Authors: J. Ignacio Cirac, David Pérez-García (ICMAT-UCM), Norbert Schuch, and Frank Verstraete
Source: Reviews in Moderns Physics vol. 93, iss. 4
Date of publication: 17 December 2021
Review:
When talking about different phases in physics, the first thing that comes to mind is the division in solid, liquid and gas, where temperature is the varying parameter which connects them through phase transition points. At zero (or close to zero) temperature, where quantum mechanics is the physical law that governs the system, there are also different phases interconnected via phase transitions. Now what usually varies is some parameter or parameters in the model under study. The exotic and unexpected properties of some of these quantum phases, like superconductivity, super fluidity, fractional statistics, topological dependency, etc. have attracted the attention of physicists for many years.
Is there a way to classify all quantum phases of matter? Solving this question has been a major program for the mathematical physics community during the last decades. The family of Projected Entangled Pair States (PEPS), introduced by Cirac and Verstraete in 2004 and rooted in the seminal work “Finitely Correlated States” by Fannes, Nachtergaele and Werner in the early 90s, has been one of the key tools to address it.
PEPS have two key properties. On the one hand, they approximate well all low energy states of quantum many body systems and then, they are complex enough to cover all quantum phases of matter. On the other hand, all the global properties of a PEPS are encoded in a particular local tensor, which can be understood as the DNA of the system, from where all global, observable, properties, can be in principle obtained.
The problem of the classification of phases reduced then to understand how global properties are characterized locally in PEPS. This local vs global behavior is a problem that appears recurrently in many areas and problems in mathematics.
The main goal of the article “Matrix product states and projected entangled pair states: Concepts, symmetries, theorems” is to review the state of the art regarding this problem. Maybe non-surprisingly, since in the end physics is all about symmetries, they are precisely the symmetries of the local tensor which make the whole plethora of exotic global properties emerge.
Of course, the whole point is to understand the relevant mathematical objects behind those symmetries, which turn out to be in this case a pretty abstract generalization of the notion of group, called weak Hopf algebras. The elementary objects in the representation theory of weak Hopf algebras can be understood precisely as particles that can fuse together generating new particles, following a set of “fusion rules”. It is precisely the behavior of those “particles” the one responsible for the global properties of the state.
The same techniques required to prove those results extend well beyond the problem of classifying quantum phases of matter. For instance, they also allow to study and classify Quantum Cellular Automata, to analyze the life-time of quantum memories, or even to design new machine learning methods with higher privacy guarantees.
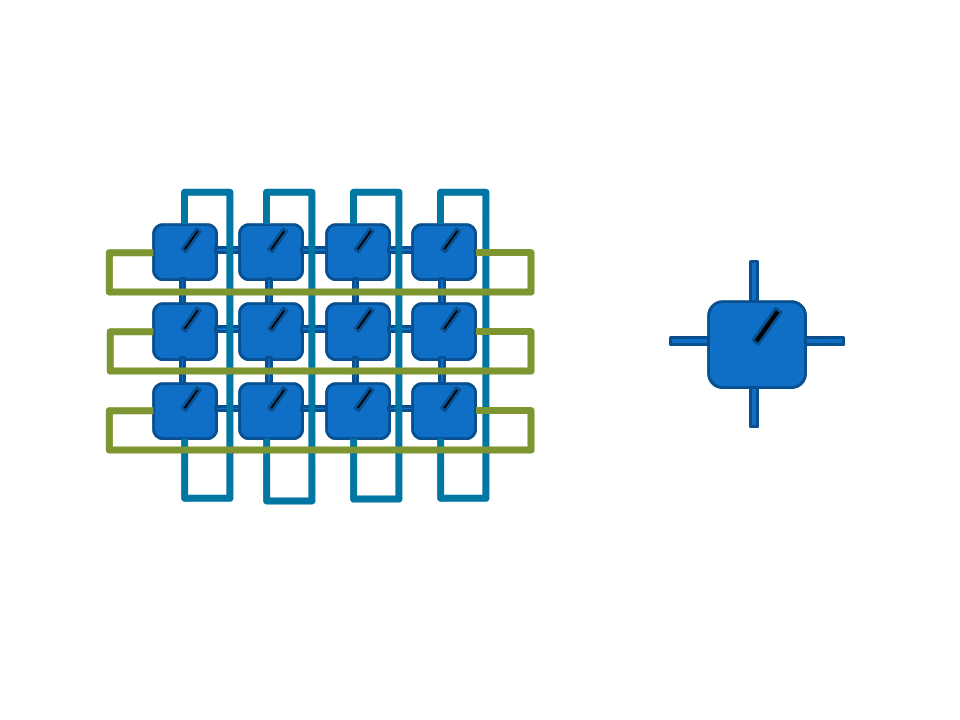
Figure: A local tensor (right), represented graphically as a box with legs associated to the different indices in the tensor, defines a global many body quantum state by contracting a Tensor Network (left) in a lattice that encodes the interactions between the different constituents of the quantum system.


