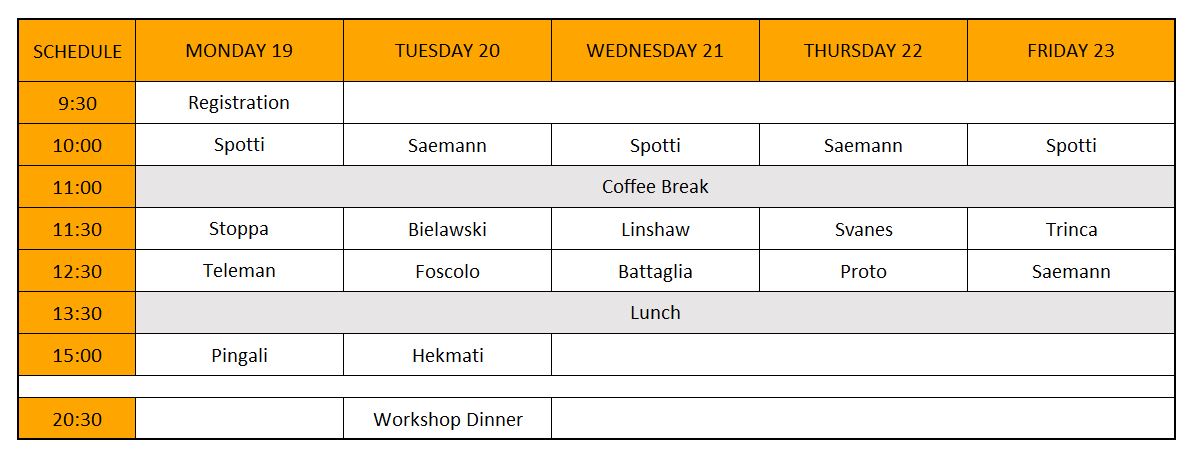
Programme
Download programme here
Titles and abstracts
Minicourses
-
Christian Saemann (Heriot-Watt): Higher principal bundles and higher gauge theory Slides
- In this course, I will provide an introduction to higher principal bundles as well as higher gauge theory and present a number of examples relevant to string theory. We will begin with higher or categorified notions of Lie groups and their Lie algebras and then turn to higher principal bundles with a focus on adjusted connections. We will apply this language to a selection of physically relevant examples, depending on interest and time: higher Chern-Simons theory, Penrose-Ward transforms, tensor hierarchies in supergravity, T-duality, and higher gauge theories related to superconformal field theories in six dimensions.
-
Cristiano Spotti (Aarhus): Geometric aspects of non-collapsed Kähler-Einstein metrics
- Canonical Kähler metrics, such as Kähler-Einstein metrics, are very important objects for the study of complex manifolds. In this minicourse, we will discuss geometric properties of such metrics on mildly singular varieties (technically, on klt pairs), focusing on topics such as the analysis of their behavior during singularity formations (e.g., tangent cones, asymptotics and bubblings) and their relevance in the study of moduli compactifications (e.g., of Fano varieties).
Research talks
-
Fiammetta Battaglia (Firenze): Nonrational toric geometry
- The geometry of toric varieties is characterized by the interplay between toric varieties and rational fans. Nonrational toric geometry concerns the extension of this setting to general fans. We give an account of nonrational toric geometry from different perspectives and present some recent developments. Based on joint work with Elisa Prato.
-
Roger Bielawski (Hannover): Coulomb branches and Nahm's equations
- Coulomb branches are putative (singular) hyperkaehler manifolds arising as (components of) moduli spaces of vacua in quantum gauge theories. In my talk I shall discuss the recent joint work with Lorenzo Foscolo, in which we propose to describe these hyperkaehler manifolds as moduli spaces of solutions to Nahm's equations.
-
Lorenzo Foscolo (UC London): Instantons on ALF spaces and codimension-1 collapse Slides
- I will discuss joint work with C. Ross aimed at describing the behaviour of Yang-Mills instantons on ALF spaces in the collapsed limit where these 4-dimensional geometries are close to a 3-dimensional collapsed limit space. In this limit, the instantons are well approximated by superpositions of simple localised building blocks constructed out of monopoles on R^3 (with singularities). I will then discuss how the construction can be used to describe the asymptotics of the hyperkähler L^2-metric on the moduli space of instantons, providing examples of a class of higher dimensional non-compact hyperkähler spaces with an asymptotic geometry, sometimes referred to as QALF, that generalises to higher dimensions the geometry of 4-dimensional ALF spaces.
-
Pedram Hekmati (Auckland): New Floer theoretic invariants of 3-manifolds
- Floer cohomology comes in various flavours and has developed into a primary tool in low-dimensional topology. In this talk, I will discuss an equivariant refinement of Seiberg–Witten–Floer cohomology for finite group actions on rational homology 3-spheres. This yields a series of numerical invariants, generalising the Ozsvath–Szabo d-invariant. I will survey their basic properties and applications in knot theory, and as obstructions to equivariant embeddings and extensions of group actions.
-
Andrew R. Linshaw (Denver): Global sections of the chiral de Rham complex for Calabi-Yau and hyperkahler manifolds Slides
- For any complex manifold M, the chiral de Rham complex is a sheaf of vertex algebras on M that was introduced in 1998 by Malikov, Schechtman, and Vaintrob. It is N-graded by conformal weight, and the weight zero piece coincides with the ordinary de Rham sheaf. When M is a Calabi-Yau manifold with holonomy group SU(d), it was shown by Ekstrand, Heluani, Kallen and Zabzine that the algebra of global sections \Omega^{ch}(M) contains a certain vertex algebra defined by Odake which is an extension of the N=2 superconformal algebra. When M is a hyperkahler manifold, it was shown by Ben-Zvi, Heluani, and Szczesny that \Omega^{ch}(M) contains the small N=4 superconformal algebra. In this talk, we will show that in both cases, these subalgebras are actually the full algebras of global sections. In an earlier work, Bailin Song has shown that the global section algebra can be identified with a certain subalgebra of a free field algebra which is invariant under the action of an infinite-dimensional Lie algebra of Cartan type. The key observation is that this algebra can be described using the arc space analogue of Weyl's first and second fundamental theorems of invariant theory for the special linear and symplectic groups. This is a joint work with Bailin Song.
-
Vamsi Pritham Pingali (IISc Bangalore): Amplitude of vector bundles and canonical metrics. Slides
- Hartshorne amplitude of vector bundles will be introduced and a generalisation of a criterion (due to Schneider and Tancredi) to recognise ample bundles will be presented. This work is joint with Indranil Biswas. We shall also introduce differentio-geometric positivity conditions and discuss PDE that are relevant for studying the Griffiths conjecture that asserts that Hartshorne ample bundles admit Griffiths positively curved metrics.
-
Yann Proto (Paris, LPTHE): Supersymmetric flows and heterotic compactifications Slides
- Geometric flows, such as Kähler–Ricci flow and its generalizations, provide powerful tools to investigate solutions of a geometric equation. In this talk, I will discuss some properties of anomaly flows, which are evolution equations for non-Kähler threefolds intimately related to solutions of the Hull–Strominger system. These flows find a natural realization as the renormalization group flow of heterotic compactifications on SU(3) structure manifolds. This allows (with a careful treatment of alpha' corrections) for a recasting of anomaly flows as gradient flows, as well as for some generalizations to higher dimensional manifolds with G2 or Spin(7) structure.
-
Jacopo Stoppa (SISSA): K-stability and mirror maps
- In the theory of mirror symmetry, the mirror of a Fano manifold X endowed with a maximally degenerate anticanonical divisor D and Kähler class [\omega] is constructed as a special type of affine fibration W: Y \to \C, called a Landau-Ginzburg model. In this talk I will show some constraints on the Landau-Ginzburg model (Y, W) which must be satisfied if the polarised mirror Fano (X, D, [\omega]) is K-(semi)stable. I will recall all the necessary notions.
-
Eirik Svanes (Stavanger): A Heterotic Kodaira-Spencer Theory at One-Loop Slides
- Taking extrema of the six-dimensional heterotic superpotential gives the so-called F-term constraints of the Hull-Strominger system. Starting at a solution, one can consider "off-shell" fluctuations of the structure in the superpotential. This gives rise to a theory with similar features to Kodaira-Spencer gravity and holomorphic Chern-Simons theory. A natural next step is then to quantise this theory. Mathematically, correlation functions in such a theory should give rise to (quasi-)topological invariants of the geometry, similar to using holomorphic Chern-Simons theory to derive Donaldson-Thomas invariants. I will discuss a first step towards such a program to derive invariants for heterotic geometries, in the quadratic approximation. This gives the one-loop partition function of the theory. Modulo complications from anomalies, this is a (quasi-)topological invariant. The anomalies are interesting in their own right, and I will discuss their resolution and implications for understanding the quantum theory.
-
Andrei Teleman (Marseille): Moduli spaces of holomorphic bundles framed along a real hypersurface Slides
- Let $X$ be a connected, compact complex manifold, and $S\subset X$ be a separating real hypersurface. $X$ decomposes as a union of compact complex manifolds with boundary $\bar X^\pm$ with $\bar X^+\cap \bar X^-=S$. Let $\mathcal{M}$ be the moduli space of $S$-framed holomorphic bundles on $X$, i.e. of pairs $(E,\theta)$ (of fixed topological type) consisting of a {\it holomorphic} bundle $E$ on $X$ endowed with a {\it differentiable} trivialization $\theta$ on $S$. This moduli space is the main object of a joint research project with Matei Toma.
The problem addressed in my talk: compare, via the obvious restriction maps, the moduli space $\mathcal{M}$ with the corresponding Donaldson moduli spaces $\mathcal{M}^\pm$ of boundary framed holomorphic bundles on $\bar X^\pm$. The restrictions to $\bar X^\pm$ of an $S$-framed holomorphic bundle $(E,\theta)$ are boundary framed formally holomorphic bundles $(E^\pm,\theta^\pm)$ which induce, via $\theta^\pm$, the same tangential Cauchy-Riemann operators on the trivial bundle on $S$. Therefore one obtains a natural map from $\mathcal{M}$ into the fiber product $\mathcal{M}^-\times_\mathcal{C}\mathcal{M}^+$ over the space $\mathcal{C}$ of Cauchy-Riemann operators on the trivial bundle on $S$.
Our result states: {\it this map is bijective}. Note that, by theorems due to S. Donaldson and Z. Xi, the moduli spaces $\mathcal{M}^\pm$ can be identified with moduli spaces of boundary framed Hermitian Yang-Mills connections.
-
Federico Trinca (Oxford): Calibrated geometry in $G_2$ manifolds with cohomogeneity two symmetry
- Constructing associative and coassociative submanifolds of a G2-manifold is, in general, a difficult task. However, when the ambient manifold admits symmetries, finding cohomogeneity-one calibrated submanifolds is more tractable. In this talk, I will discuss joint work with B. Aslan regarding the geometry of such calibrated submanifolds in G2-manifolds with a non-abelian cohomogeneity two symmetry. Afterwards, I will explain how to apply these results to describe new large families of complete associatives in the Bryant--Salamon manifold of topology $S^3×ℝ^4$ and in the manifolds recently constructed by Foscolo--Haskins—Nördstrom.




