Inaugural Colloquium (13/03/2019):
Speaker: Joachim Cuntz, WWU Münster, Germany.
Title: The ring of integers and C*-algebras.
Abstract: Among the most basic structures in mathematics are the sets of natural numbers and of integers with their operations of addition and multiplication. These structures give rise, in a completely natural way, to C*-algebras with intriguing properties. The study of these C*-algebras and in particular of their K-theoretical invariants reveals close connections with algebraic number theory. These connections can be extended, from the usual ring of integers to rings of algebraic integers in number fields.
School I (11-15/03/2019):
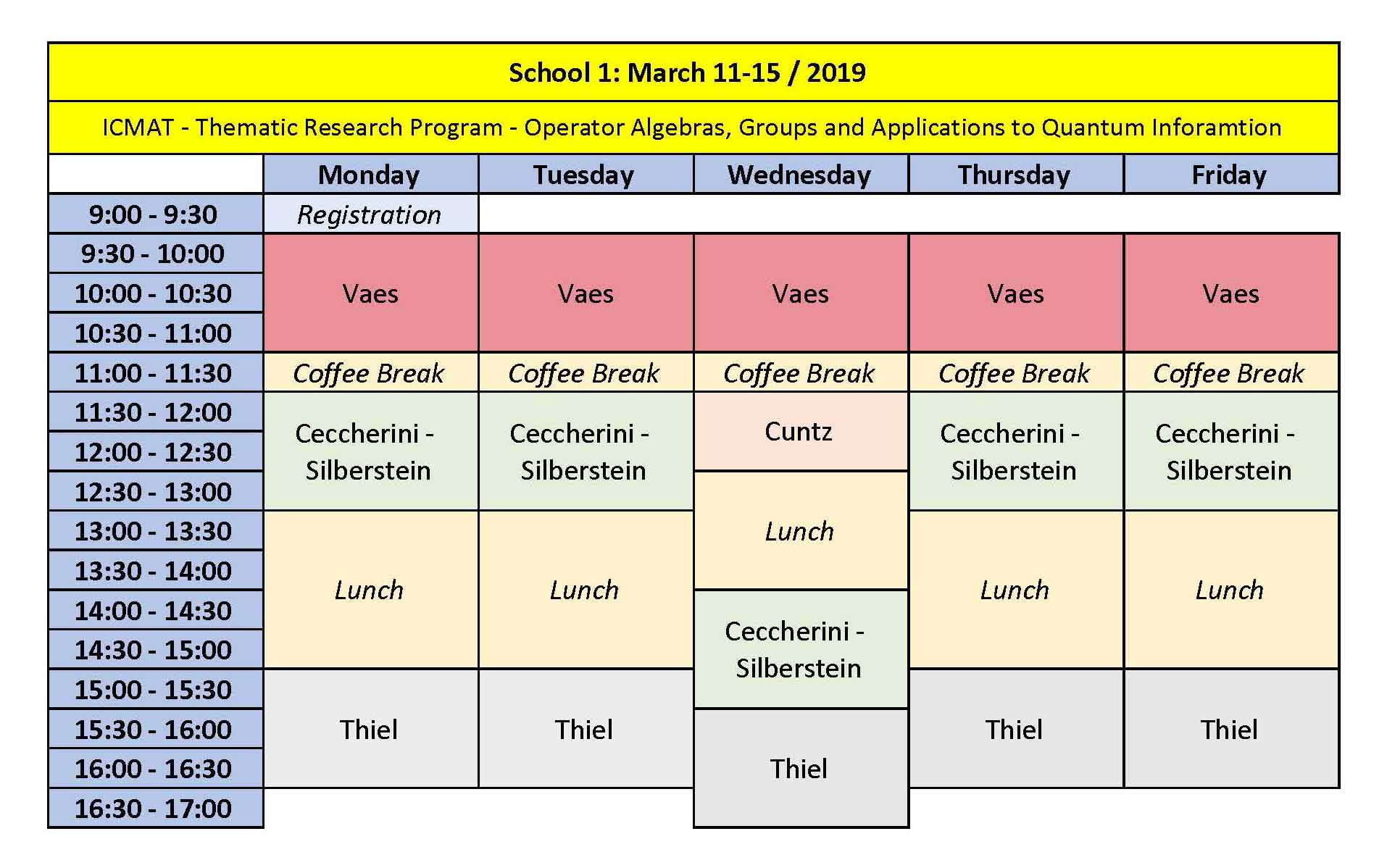

The aim of this school is to introduce and develop several topics around the classification of operator algebras and amenability of groups and spaces. The school will be divided into three courses:
-
Course I: Stefaan Vaes (KU-Leuven, Belgium)
Title: Type III factors, free Araki-Woods factors and their (non-)classification
Abstract: The course starts with a basic introduction to von Neumann algebras of type III, the modular theory of Tomita-Takesaki and Connes' classification of amenable factors. I then introduce Shlyakhtenko's free Araki-Woods factors, which are free probability analogs of the injective type III factors. I present Shlyakhtenko's classification of the almost periodic free Araki-Woods factors and the more recent non almost periodic classification results from a joint work with Houdayer and Shlyakhtenko. I will finally show that this also gives rise to unclassifiably many nonisomorphic free Araki-Woods factors (joint work with Sasyk and Törnquist). -
Course II: Tullio Ceccherini-Silberstein (U. Sannio, Italy)
Title: Amenability of groups.
Abstract: In these lectures, I would like to present the notion of amenability (of discrete groups), introduced in 1929 by John von Neumann in relation to the study of the Banach-Tarski paradox. Since then, the notion of amenability has been extended to other different settings and nowadays plays a fundamental role in Harmonic Analysis, Functional Analysis, and Operator Algebras, in Geometric and Combinatorial Group Theory, in Ergodic Theory and Dynamical Systems, as well as in Probability, Statistical Mechanics, and Mathematical Physics. I'll present some characterizations of amenability (for discrete groups), combining methods from Functional Analysis, Combinatorics & Graph Theory, Probability & Random Walks, Combinatorial and Geometric Group Theory, and Dynamical Systems.Time permitting, I'll also discuss the notion of amenability for discrete metric spaces.PROGRAMME:
- Definitions, examples, and properties of the class of amenable groups.
- The Folner condition
- Paradoxical decompositions and the Tarski alternative theorem (including the Rado-Hall marriage theorem for bipartite graphs).
- The Markov-Kakutani type theorem for amenable groups.
- The Kesten criterion.
- The Grigorchuk cogrowth criterion.
- The Ornstein-Weiss theorem and applications: entropies.
- Cellular automata and the Garden of Eden theorem for amenable groups.
- Amenability for discrete metric spaces.
-
Course III: Hannes Thiel (WWU-Münster, Germany)
Title: Structure and classification of amenable C*-algebras.
Abstract: A series of spectacular breakthroughs over the past three years led to the completion of the decades-long effort to classify simple, amenable C*-algebras by K-theory. We will discuss these results and the connections to the regularity conjecture of Toms-Winter on the structure of simple, amenable C*-algebras. We will also study the Cuntz semigroup, which is a geometric refinement of K-theory that has been used to obtain structure and classification results for non-simple C*-algebras.
Workshop I (18-22/03/2019):
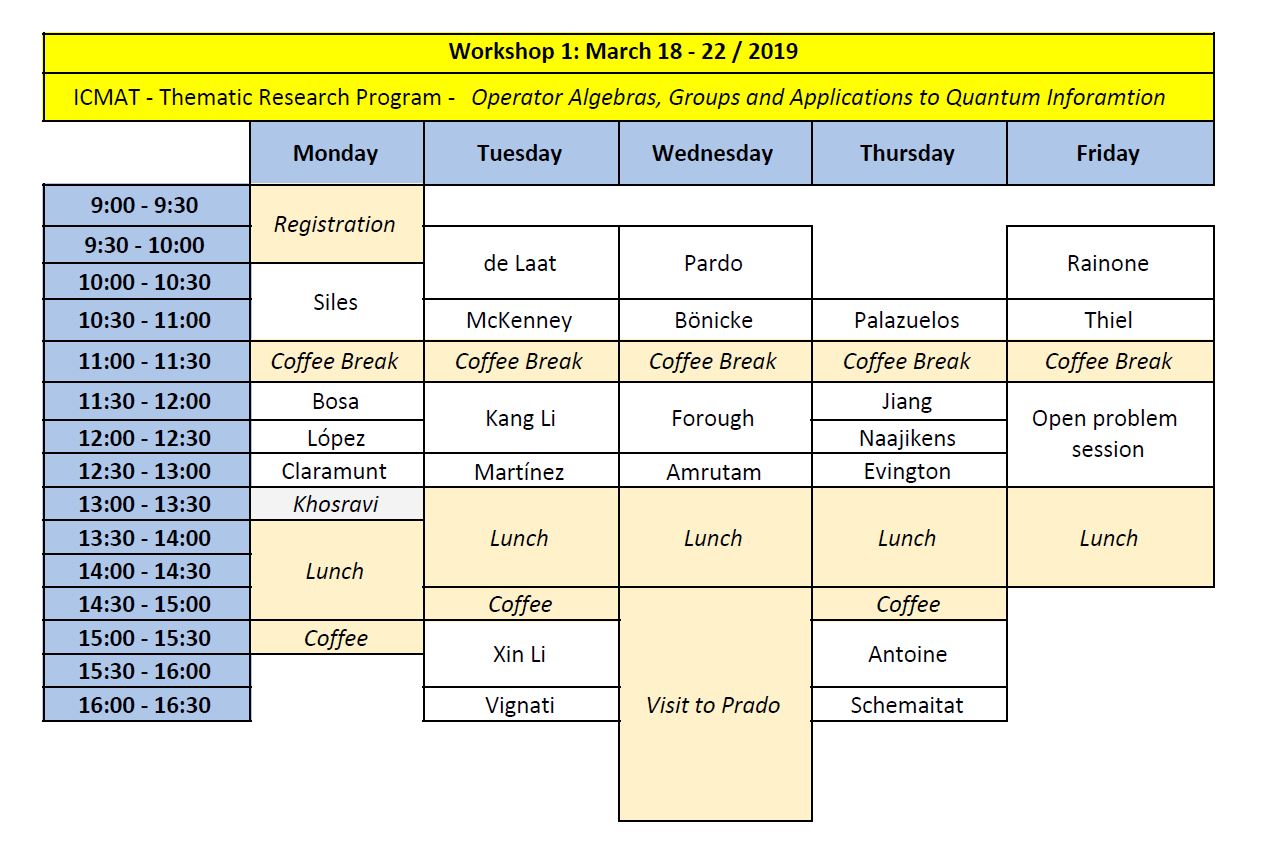
Talks - 50 minutes
- Mercedes Siles (U. Málaga); A new look at evolution algebras.
- Pere Ara (U. Autónoma de Barcelona); Separated graphs and dynamics.
- Tim de Laat (WWU-Münster); Fixed point properties for group actions on Banach spaces.
- Kang Li (IMPAN – Warsaw); Rigidity of L^p-uniform Roe algebras.
- Xin Li (Queen Mary U., London); Constructing Cartan subalgebras in classifiable C*-algebras.
- Enrique Pardo (U. Cádiz); Simplicity of algebras associated to non-Hausdorff groupoids.
- Marzieh Forough (IPM, Iran and Check Academy of Sciences); Weak tracial Rokhlin property for finite group actions on simple C*-algebras.
- Ramón Antoine, (UAB); The Cuntz Semigroup of Stable Rank One C*-algebras.
- Timothy Rainone (U. Arizona, USA); The type semigroup construction.
Talks - 30 minutes
- Joan Bosa (UAB); The nuclear dimension of 𝒪∞-stable C*-algebras.
- Diego López (ICMAT-UAM); The strong Atiyah conjecture for locally indicable groups.
- Joan Clarmunt (UAB); Uniqueness of the von Neumann continuous factor.
- Fatemeh Khosravi (IPM, Iran); A Kawada-Ito theorem for locally compact quantum groups.
- Paul McKenney (Miami U. Ohio, USA); Rigidity of corona algebras.
- Diego Martínez (ICMAT-UC3M); Inverse semigroup Roe Algebras.
- Alessandro Vignati (KU-Leuven); Rigidity conjectures in C*-algebras.
- Christian Bönicke (U. Glasgow); A going-down principle for ample groupoids.
- Tattwamasi Amrutam (U. Houston, USA); Simplicity of Intermediate C*-algebras.
- Carlos Palazuelos, (UCM-ICMAT); Grothendieck Theorem for biliear forms on C*-algebras with applications to Quantum Information Theory.
- Yongle Jiang (IMPAN, Warsaw); Continuous cocycle superrigidity for full shifts and groups with one end.
- Pieter Naaijkens (UCM); Quantum channels from subfactors.
- Samuel Evington (U. Glasgow); The Classification of C*-Algebras and the Toms–Winter Conjecture.
- Andre Schemaitat (WWU-Münster); The Jiang-Su algebra is strongly self-absorbing, revisited.
- Hannes Thiel (WWU-Münster); Inductive limits of semiprojective C*-algebras.