Horizons of Mathematics, with Motohico Mulase (University of California Davis (USA))

Motohico Mulase is an expert in integrable systems, complex algebraic geometry, complex analysis, mathematical physics and differential geometry.

Motohico Mulase (University of California Davis (USA)) is the speaker at the ICMAT-UAM-UCM-UC3M Joint Colloquium on 11 October. His talk, ‘Miraculous Integer Sequences’ explores two fascinating sequences of integers: that of Catalan numbers and that of Gromov-Witten invariants of genus 0 of a certain algebraic variety. In them, there are connections with cosmology, quantum physics and the mysterious Riemann zeta function. The event is at 13:00 in the Aula Magna Miguel de Guzmán of the Faculty of Mathematics of the Complutense University of Madrid and can also be followed online at the following link.

Ágata Timón García-Longoria (ICMAT)

At school we are taught sequences –i.e. ordered collections– of integers: the sequence of even numbers, or odd numbers, the sequence of primes, the sequence of perfect squares… Some are particularly interesting, such as, for example, the famous Fibonacci sequence: (1, 1, 2, 3, 5, 8, …). In its terms –each of them is constructed by adding the two previous ones–, the famous golden number emerges –as the Fibonacci sequence progresses, the division of two consecutive terms gets closer and closer to this irrational value–. In addition, this collection of numbers also appears in numerous natural phenomena, for example, when observing the growth patterns of leaves, flower petals and branches of plants, or the distribution of seeds in sunflowers. Mathematician Motohico Mulase, a researcher at the University of California Davis (USA), is an expert in this type of sequences and in discovering their most amazing properties.

One of the sequences studied by Mulase is the Catalan numbers sequence. ‘These numbers appear in many combinatorial problems, and also in classifying black holes in astrophysics’ explains Mulase. ‘The generating function of the Catalan numbers [in the image below] satisfies a differential equation, and if you apply a simple transformation on it –the Laplace transform, which corresponds to what is called the mirror symmetry–- you get another differential equation: its mirror-symmetric partner. Well, this symmetric equation turns out to be a Schrödinger equation,” Mulase says. It is one of the fundamental equations of quantum mechanics, which describes how the quantum state of a physical system evolves over time. ‘The most fascinating thing is that this equation knows the topology of the so-called moduli spaces of all Riemann surfaces,’ he adds.

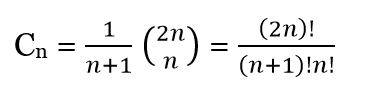
The Catalan numbers can be obtained by the following formula, giving n natural values.

Another sequence of integers he has investigated is that of Gromov-Witten invariants of genus 0 of a certain algebraic variety. “These quantities have their origin in quantum field theory,” says Mulase. ‘When we look up at the night sky, we wonder about the vastness of the universe and its amazing beauty. The desire to understand our universe better led physicists to discover a new set of indicators of the structure of the universe: the Gromov-Witten invariants,” he says. “These quantities are originated in quantum field theory, and acquired into mathematics as a new type of indicator of symplectic geometry” he says.

“Surprisingly, this integer sequence was actually discovered nearly a half century ago by a number theorist Roger Apéry in his proof of the irrationality of the special value of the Riemann zeta function at 3,” Mulase says. “The Riemann zeta function is one of the most mysterious functions, and almost nothing is known for its values of positive odd integers. Only for the value at 3, we know it is irrational, due to Apéry’s proof,” says the mathematician.

Key to proving this profound result was the same sequence of integers devised by the theoretical physicists. “He used the same integer sequence to construct a rapidly convergent rational sequence approximating zeta function in 3. The convergence of this approximation is too fast, and a simple theorem in number theory tells us immediately that zeta function in 3 has to be irrational,” he explains.

“Although zeta funtion in 3 appears in many places in physics –such as the anomalous magnetic moment of electron– and in geometry, we are observing a different story: The symplectic invariant of a geometric space seems to know the irrationality of Zeta(3)!,” exclaims.

“Looking up at the starry skies in the night, we feel many frontiers of modern mathematics, and the deep interplay between geometry, number theory, differential equations, and topology. The skies are inviting us to appreciate the hidden beauty among many different parts of mathematics and their intertwined whole,” concludes.

Motohico Mulase

Motohico Mulase was born in Kanazawa, Japan. He graduated from the University of Tokyo and obtained a Doctor of Science degree from Kyoto University. After a short period teaching in Nagoya University, he moved to the United States in 1982, as a Fellow at Harvard University. He took positions at the Mathematical Sciences Research Institute, Berkeley; Stony Brook University; UCLA; and the Institute for Advanced Study, Princeton. Then in 1989, he received a tenured position at the University of California, Davis. He has been Full Professor there since 1991. Mulase served as Chair of the Department of Mathematics at UC Davis for 6 years. He also served as Associate Dean of the Faculty for Mathematical and Physical Sciences, in charge of all personnel actions in 5 departments: Chemistry, Earth and Planetary Science, Mathematics, Physics and Astronomy, and Statistics. Since 2019, he is a Distinguished Professor of Mathematics at UC Davis. He has taken numerous visiting positions, including Max-Planck-Intitut für Mathematik in Bonn and l’Institut des Hautes Études Scientifiques in Paris.

Abstract:

In this Colloquium, I will survey two such sequences, and explain their unexpected miracles.

The first one is the Catalan numbers. I will explain how this integer sequence leads us to two differential equations, their mirror-symmetric relations, and the quantization behind the scenes. We present Lauren polynomials that give solutions to these equations.

The miracle here is that these Laurent polynomials know the topological invariants of the moduli space of pointed Riemann surfaces, calculated by Harer-Zagier, Witten, and Kontsevich.

The second example is analogous to the first one in the sense that it is an integer sequence of genus 0 Gromov-Witten invariants of a particular algebraic 3-fold. We have again two differential equations. The contrast is that although we know mirror symmetric and quantization relation between these equations, the key mechanism to calculate general GW invariants is still missing. The miracle here is that this particular integer sequence knows why Riemann zeta at 3 is irrational, the work of Apery.