A paper published last Friday in PNAS, authored by Alberto Enciso and Daniel Peralta-Salas, researchers at CSIC in ICMAT, presents flows whose equilibrium is disrupted by any small perturbation. Their proof refutes, in three dimensions, a conjecture that claimed the impossibility of such flows. “This changes the way we think about the structure of a fluid in equilibrium,” say Enciso and Peralta.

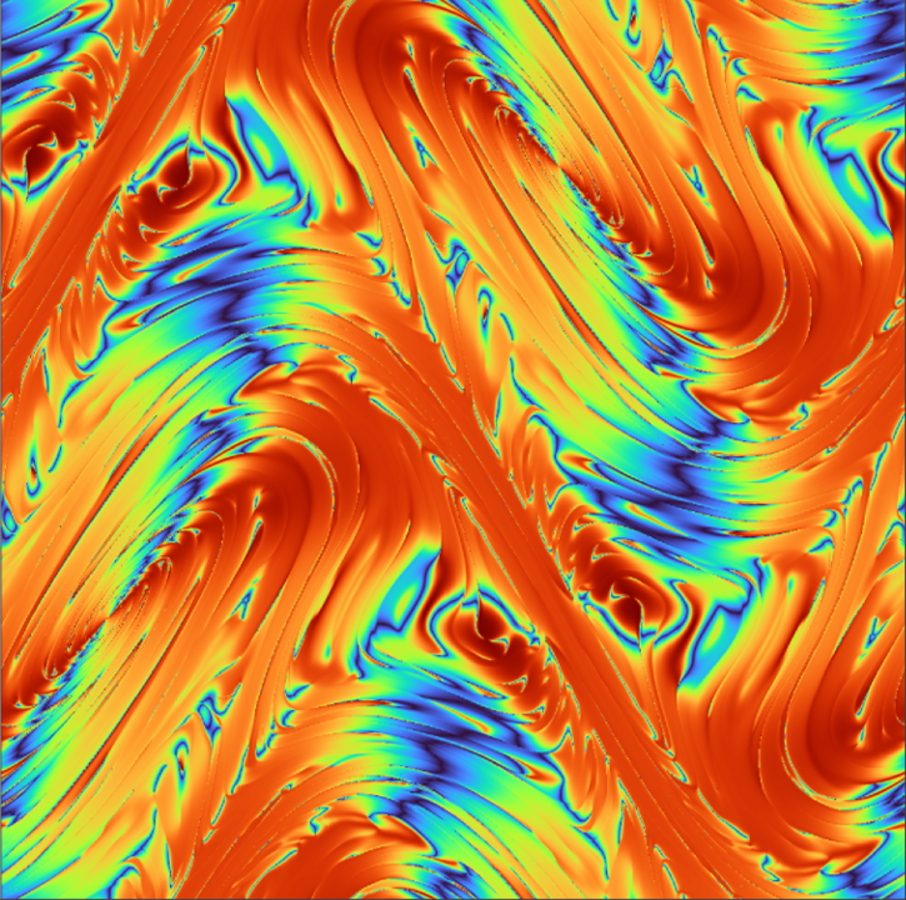
The image shows a two-dimensional cross-section of a three-dimensional turbulent flow. Image: Terry Brannigan.

It might seem that in an equilibrium fluid—whose structure does not change over time—only simple patterns emerge. For example, in water flowing through a pipe at a constant speed, the streamlines apparently indicate the movement of each fluid particle. However, beneath the visible tranquility, intricate behaviors may be hidden, which the research community strives to understand. “The goal is to decipher how complex these types of fluids, known as stationary, can be,” explain Alberto Enciso and Daniel Peralta-Salas, researchers at the Spanish National Research Council (CSIC) at the Institute of Mathematical Sciences (ICMAT). In an article published on 21 March in the Proceedings of the National Academy of Sciences of the United States of America (PNAS), these researchers, together with Willi Kepplinger (University of Vienna, Austria), demonstrate that the complexity is much greater than previously thought.

For the first time, scientists have theoretically proven the existence of stationary flows in which any small perturbation, such as a slight pressure change, radically alters their behavior, pulling them out of equilibrium and potentially leading to highly complex and unpredictable behaviors: turbulence. These are known as isolated stationary flows.

“This changes the way we think about the structure of a fluid in equilibrium,” they state. Until now, the research community was only aware of non-isolated stationary flows, leading Theodore Drivas (Stony Brook University, USA) and Tarek Elgindi (Duke University, USA) to conjecture that in two dimensions, stationary flows are never truly stationary. The PNAS study proves that in three dimensions—like the world we live in, where uncertainty is even greater due to the complexity of systems—the behavior is entirely different: the Drivas-Elgindi conjecture is false.

“We have demonstrated that there is a very broad range of three-dimensional isolated stationary fluids. In fact, we prove that most equilibrium states are isolated,” they affirm. In two dimensions, the conjecture remains open. “It is known that, in two dimensions, equilibrium fluids are generally non-isolated, but the question is whether all of them share this property, as we now know is not the case in three dimensions,” the mathematicians explain. This stark difference in behavior between dimensions is common and observed in many mathematical and real-world contexts. “For example, wave propagation is also radically different in two and three dimensions, due to a classical effect known as Huygens’ principle,” they describe.

The oldest and most challenging equations

“The great challenge is to fully understand the set of equilibrium solutions to these equations, which describe fluids, and the relationships between them—that is, the ‘sociology’ of this space,” they add.

Fluid motion is mathematically described by a system of equations proposed by mathematician Leonhard Euler in the 18th century, derived from applying Newton’s laws to fluids. “It is the second-oldest partial differential equation we know—the only older one is the one describing wave propagation—and one of the most studied throughout history, yet it continues to pose significant challenges for the international scientific community,” the mathematicians state.

Through a combination of differential geometry and dynamical systems techniques, which are rarely used in fluid mechanics studies, the researchers have managed to understand the mechanism leading to isolation.

“The isolated stationary solutions we constructed are highly chaotic. When we sent our work to Theo Drivas, he responded immediately, fascinated. He offered us a popular interpretation of our result: chaotic behavior makes it difficult to have friends. Nothing could be truer, both in fluids and in real life,” the scientists conclude.

This content has been automatically translated. The original text may differ slightly.