The Horizons of Mathematics, with Elizabeth Gillaspy (University of Montana, USA)

Elizabeth Gillaspy is a researcher at the University of Montana (USA). Image: Elizabeth Gillaspy.

Ágata Timón G Longoria (ICMAT-CSIC). Shifts of finite type can be expressed in terms of a graph; therefore, they can be studied using tools from graph theory, matrix theory, and dynamics. Understanding when two of them are essentially the same is a central question in the field but is unfortunately extremely hard in general. In some cases, this can be done in a more straightforward and computable way. Now, Elizabeth Gillaspy (University of Montana, USA) and her collaborators have discovered a new class where this is the case: meteor graphs. At the recent Joint Mathematics Colloquium, Gillaspy presented this result and the techniques used in its proof, which she hopes will help identify more classes of graphs (or finite-type shifts) of this nature.

We are surrounded by graphs: the subway map or representations of activity in a social network are common examples. These are simple mathematical objects composed of elements (or nodes) and relationships between them (edges). “For example, the network of who-follows-whom on X or Instagram is a directed graph. The users of the platform are the nodes of the network; we put an edge from node v to node w if v follows w. Note that the direction of the edge is important; I may follow Beyonce, but she probably does not follow me!” explains Elizabeth Gillaspy, professor at the University of Montana (USA) and speaker at the Joint Mathematics Colloquium, which took place at the end of last January and is now available online.

In any graph, when considering the set of all two-sided infinite (directed) paths in the graphs—that is, routes to reach one vertex from another following the available edges—, we obtain an object belonging to the field of dynamical systems: a shift of finite type. Moreover, it turns out that any shift of finite type can be described as the shift space associated with a directed graph. Thus, directed graphs and finite-type shifts are two sides of the same coin.

“Shifts of finite type, therefore, are a particularly tractable class of shift spaces—they can be studied via the definition of the shift space; via the associated graph; and also via the adjacency matrix of the graph,” describes Gillaspy. “That is, we can use tools from graph theory, matrix theory, linear algebra, and dynamics to study shifts of finite type.”

When studying and classifying finite-type shifts, it is essential to determine when two shifts are essentially the same. “As mathematicians, we often want to understand when two objects which are presented differently actually have the same mathematical structure,” Gillaspy explains. For example, the set of integers and the set of natural numbers are the same, because both sets, element by element, can be put in correspondence – mathematically, we say that there is a bijection between them. “In the context of shifts of finite type, there’s more structure that we want to keep track of: namely, a metric (that is, a notion of distance) and something called the shift map. So, we say that two shifts of finite type are ‘the same,’ or conjugate, if there’s a bijection between them that also preserves the metric and the shift map.”

It is possible to determine whether two finite-type shifts are conjugate by studying the adjacency matrices of their corresponding graphs. ‘In 1973, Robert F. Williams defined the notions of shift equivalence (SE) and strong shift equivalence (SSE) for finite-type shifts, using the adjacency matrices of the associated graphs.  He then showed that two finite-type shifts are conjugate if and only if their adjacency matrices are SSE’, says Gillaspy.

However, checking whether or not two matrices are SSE is not always easy.  “For example, it’s not known whether matrices A, with rows (1, 4) and (3, 1) and B, with rows (1, 12) and (1, 1) are either SSE or not’, the mathematics shows.

On the other hand, checking whether two matrices are SE or not is a relatively straightforward computation. Could we, based on this information, determine whether the matrices are also SSE? In 1973, Williams claimed that SE and SSE were always equivalent. However, a year later, he discovered a flaw in his proof. Additionally, two decades later, Ki Hang Kim and Fred Roush found examples of matrices that are SE but not SSE, proving that SE and SSE (and, therefore, conjugacy) do not always coincide. “Still, it’s worth finding classes of matrices (equivalently, directed graphs, or shifts of finite type) where SE and SSE coincide. In these situations, conjugacy (SSE) is computable.”

Gillaspy and her collaborators have identified a new class of this type: meteor graphs. “A meteor graph is a directed graph which consists of two cycles (the source cycle and the sink cycle) and some directed paths connecting them, where all of these paths run from the source cycle to the sink cycle.”

“Sin embargo, comprobar si dos matrices son SSE no siempre es fácil. Por ejemplo, no se sabe si las dos matrices A, con filas (1, 4)  y (3, 1)  y B, con filas (1, 12) y (1, 1) son SSE o no”, muestra la matemática.

En cambio, comprobar que dos matrices son SE o no, sí supone un cálculo relativamente fácil. ¿Podríamos, a partir de esta información, saber si las matrices son también SSE? En 1973, Williams afirmó que sí: las nociones de SE y SSE eran siempre equivalentes. Pero un año más tarde, descubrió un fallo en su demostración. Adicionalmente, dos décadas más tarde, Ki Hang Kim y Fred Roush encontraron ejemplos de matrices que son SE, pero no SSE, por lo que sabemos que SE y SSE (y, por tanto, la conjugación) no coinciden en todos los casos.  “Se sabe que, como sugieren sus nombres, siempre que dos matrices son SSE, también son SE. Pero, de momento, sigue sin saberse en qué circunstancias si dos matrices son SE también son SSE”, explica Gillaspy.

La comunidad investigadora busca clases de matrices (o, equivalentemente, grafos dirigidos o desplazamientos de tipo finito) en las que SE y SSE coincidan y, por tanto, la conjugación SSE sea computable. Gillaspy, con sus colaboradores, ha identificado una nueva clase de este tipo: la de los grafos meteóricos. “Un grafo meteórico es un grafo dirigido que consta de dos ciclos (el ciclo origen y el ciclo sumidero) y unos caminos dirigidos que los conectan, donde todos estos caminos van del ciclo origen al ciclo sumidero”, define Gillaspy.

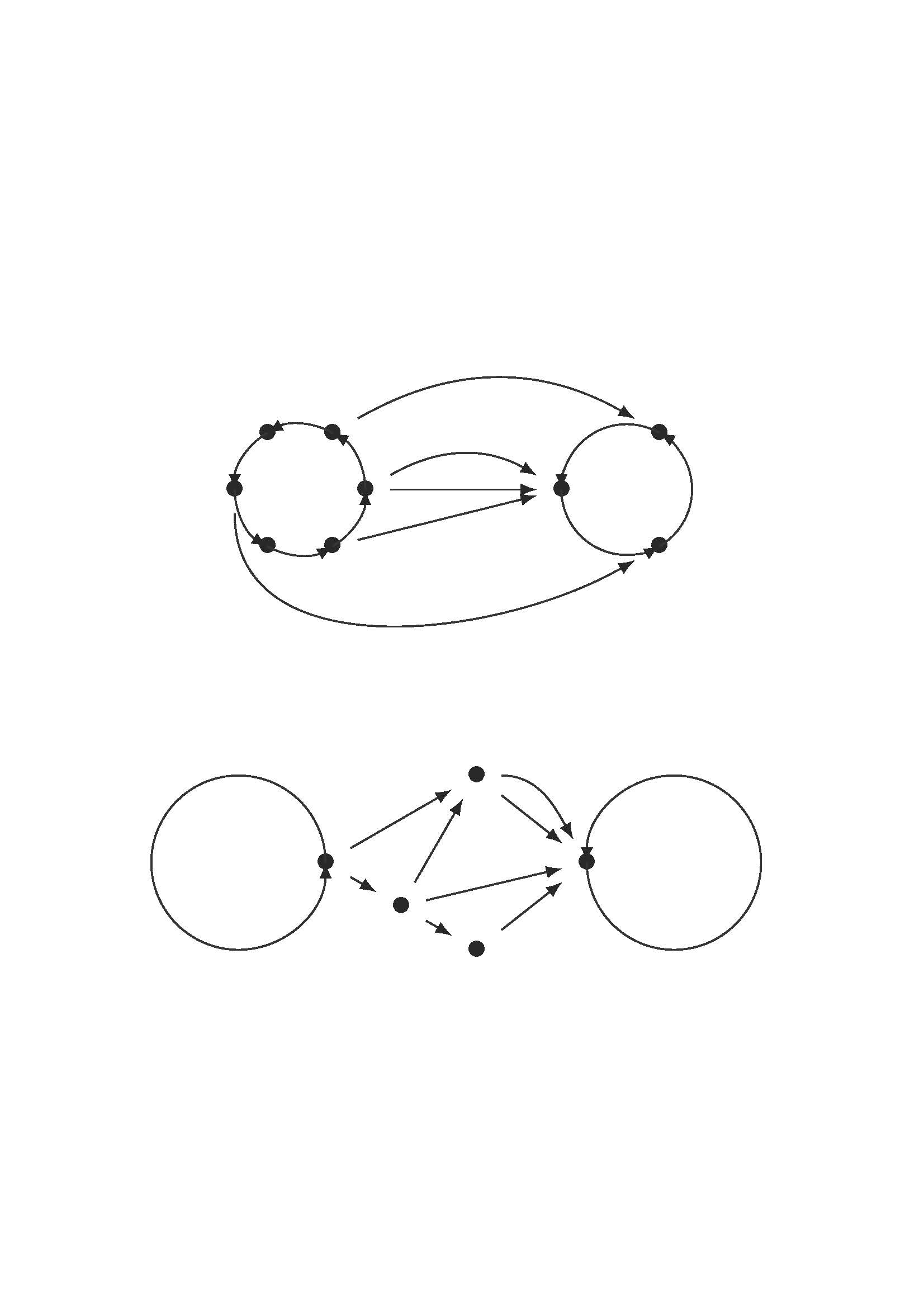
Ejemplos de grafos meteóricos. Imagen: Elizabeth Gillaspy.

They have demonstrated that the structural restrictions of meteor graphs force these two concepts to coincide. “The key to our proof is that, graphically, we understand quite well how SSE works; and algebraically, we understand quite well how SE works,” explains Gillaspy. “Two directed graphs are SSE if and only if you can turn one graph into the other using insplitting and outsplitting. The structure of the meteor graphs puts limits on how much in- and out-splitting can change the graph, so we can describe exactly when two meteor graphs are SSE.”

“On the other hand, two graphs are SE if and only if their ‘talented monoids’ are graded isomorphic; this is a statement about algebraic objects, which can be computed from the adjacency matrices of the graphs. What we proved is that this isomorphism of talented monoids occurs precisely when the meteor graphs are SSE.”

Now, the researcher hopes that the proof strategy used for meteor graphs will help verify that SE is equivalent to SSE for more classes of graphs (or, equivalently, finite-type shifts).