Los horizontes de las matemáticas, con Elizabeth Gillaspy (Universidad de Montana, EE. UU.)

Elizabeth Gillaspy es investigadora en la Universidad de Montana (EE UU). Imagen: Elizabeth Gillaspy.

Ágata Timón G Longoria (ICMAT). Los desplazamientos de tipo finito pueden expresarse en términos de un grafo, por tanto, es posible estudiarlos mediante herramientas de la teoría de grafos, de la teoría matricial y de la dinámica. Entender cuándo dos de ellos son, esencialmente, iguales es una cuestión central del campo. En algunos casos, esto puede hacerse de forma más sencilla, computable, pero, por desgracia, es extremadamente difícil en general. Ahora, Elizabeth Gillaspy (Universidad de Montana, EE. UU.) y sus colaboradores han encontrado una nueva clase en la que es así: los grafos meteóricos. En el pasado Coloquio Conjunto de Matemáticas, celebrado a finales de enero, Gillaspy presentó este resultado y las técnicas de su demostración que, espera, permitan localizar más clases de grafos (o desplazamientos de tipo finito) de este tipo.

Vivimos rodeados de grafos: el plano del metro o la representación de la actividad en una red social son ejemplos habituales. Se trata de sencillos objetos matemáticos formados por elementos (nodos) y relaciones entre ellos (vértices): “Por ejemplo, la red de quién-sigue-a-quién en X o Instagram es un grafo dirigido, los usuarios de la plataforma son los nodos de la red; y existe una arista del nodo v al nodo w si v sigue a w. La dirección de la arista es importante; yo puedo seguir a Beyoncé, pero probablemente ella no me siga a mí”, explica Elizabeth Gillaspy, profesora de la Universidad de Montana (EE. UU.) y ponente del Coloquio Conjunto de Matemáticas que se celebró a finales del pasado mes de enero y ahora está disponible online.

En cualquier grafo, al considerar el conjunto formado por todos los caminos dirigidos –es decir, las rutas para llegar de un vértice a otro siguiendo las aristas disponibles–, infinitos en ambas direcciones, se obtiene un objeto perteneciente al área de los sistemas dinámicos: un desplazamiento (shift) de tipo finito. Y, es más, resulta que cualquier desplazamiento de tipo finito se corresponde con el espacio de desplazamiento asociado a un grafo dirigido. Por tanto, grafos dirigidos y desplazamiento de tipo finito son dos caras de la misma moneda.

“Los desplazamientos de tipo finito son, por tanto, una clase de espacios de desplazamiento particularmente manejable: pueden estudiarse a través de su propia definición, a través del grafo asociado y también a través de la matriz de adyacencia del grafo”, describe Gillaspy. “Es decir, podemos estudiarlos mediante herramientas de la teoría de grafos, de la teoría matricial y del álgebra lineal y de la dinámica”.

Al estudiar y clasificar los desplazamientos de tipo finito es interesante saber cuándo dos desplazamientos son, esencialmente, el mismo. “En matemáticas, a menudo queremos entender cuándo dos objetos, que se presentan de manera diferente, en realidad tienen la misma estructura matemática”, detalla Gillaspy.  Por ejemplo, el conjunto de los números enteros y el conjunto naturales son iguales, porque ambos conjuntos, elemento a elemento, se pueden poner en correspondencia –matemáticamente, decimos que hay una biyección entre ellos–.  “En el contexto de los desplazamientos de tipo finito, también hemos de tener en cuenta la estructura, que viene dada por una métrica (es decir, una noción de distancia) y algo llamado mapa de desplazamiento.  Así, dos desplazamientos de tipo finito son iguales, o conjugados, si hay una biyección entre ellos que también preserve la métrica y el mapa de desplazamiento”, afirma.

Es posible determinar si dos desplazamientos de tipo finito son conjugados estudiando las matrices de adyacencia de sus grafos correspondientes. “En 1973, Robert F. Williams definió las nociones de equivalencia de desplazamiento (SE) y equivalencia fuerte de desplazamiento (SSE) para los desplazamientos de tipo finito, utilizando las matrices de adyacencia de los grafos asociados.  Después, demostró que dos desplazamientos de tipo finito son conjugados si y sólo si sus matrices de adyacencia son SSE”, relata Gillaspy.

“Sin embargo, comprobar si dos matrices son SSE no siempre es fácil. Por ejemplo, no se sabe si las dos matrices A, con filas (1, 4)  y (3, 1)  y B, con filas (1, 12) y (1, 1) son SSE o no”, muestra la matemática.

En cambio, comprobar que dos matrices son SE o no, sí supone un cálculo relativamente fácil. ¿Podríamos, a partir de esta información, saber si las matrices son también SSE? En 1973, Williams afirmó que sí: las nociones de SE y SSE eran siempre equivalentes. Pero un año más tarde, descubrió un fallo en su demostración. Adicionalmente, dos décadas más tarde, Ki Hang Kim y Fred Roush encontraron ejemplos de matrices que son SE, pero no SSE, por lo que sabemos que SE y SSE (y, por tanto, la conjugación) no coinciden en todos los casos.  “Se sabe que, como sugieren sus nombres, siempre que dos matrices son SSE, también son SE. Pero, de momento, sigue sin saberse en qué circunstancias si dos matrices son SE también son SSE”, explica Gillaspy.

La comunidad investigadora busca clases de matrices (o, equivalentemente, grafos dirigidos o desplazamientos de tipo finito) en las que SE y SSE coincidan y, por tanto, la conjugación SSE sea computable. Gillaspy, con sus colaboradores, ha identificado una nueva clase de este tipo: la de los grafos meteóricos. “Un grafo meteórico es un grafo dirigido que consta de dos ciclos (el ciclo origen y el ciclo sumidero) y unos caminos dirigidos que los conectan, donde todos estos caminos van del ciclo origen al ciclo sumidero”, define Gillaspy.

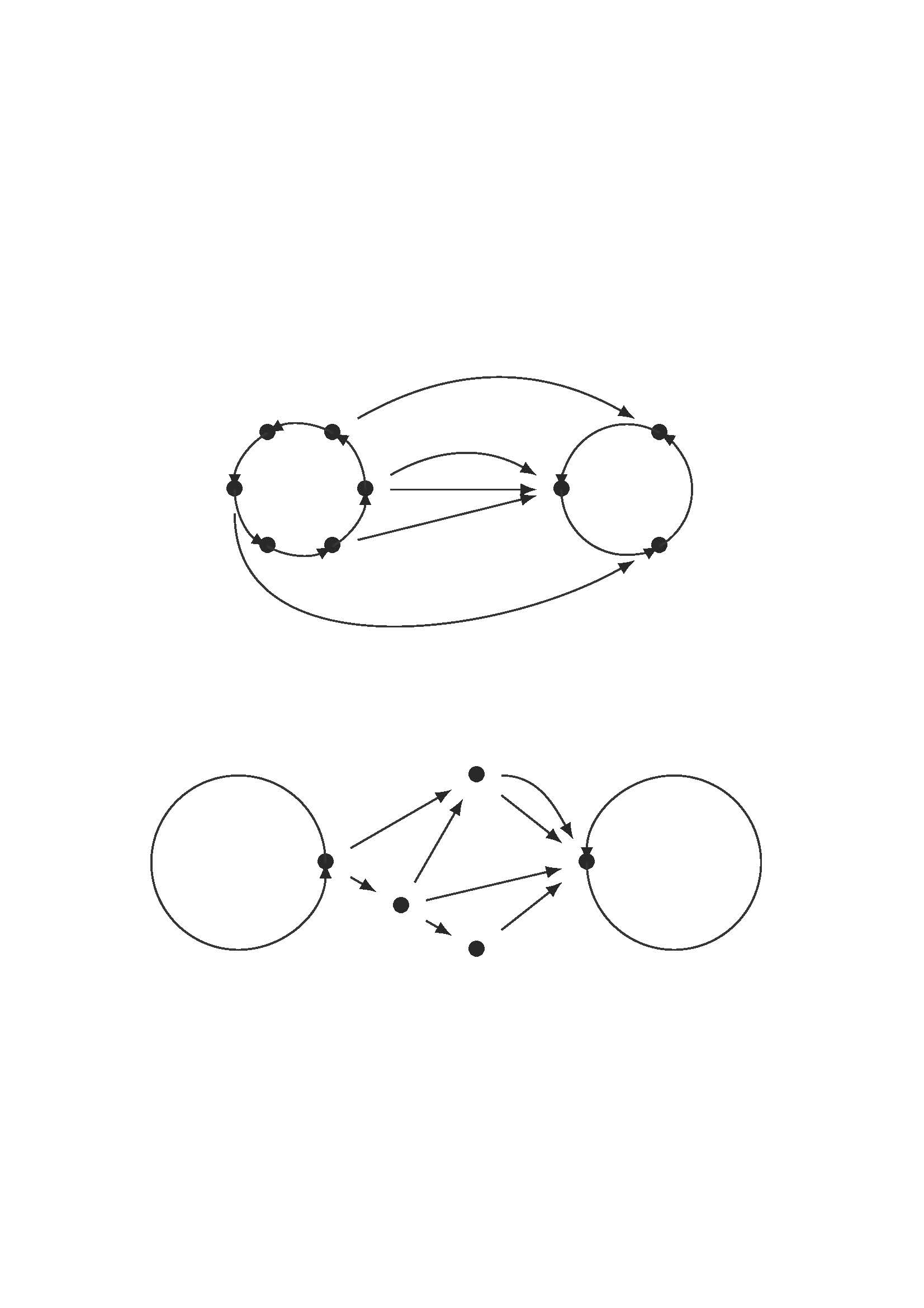
Ejemplos de grafos meteóricos. Imagen: Elizabeth Gillaspy.

Han demostrado que las restricciones estructurales de los grafos meteóricos obligan a que estos dos conceptos coincidan. “La clave de nuestra prueba es que, gráficamente, entendemos bastante bien cómo funciona SSE; y algebraicamente, entendemos bastante bien cómo funciona SE”, relata. “En concreto, dos grafos dirigidos son SSE si y sólo si se puede convertir un grafo en el otro utilizando dos técnicas (insplitting y outsplitting). La estructura de los grafos meteóricos pone límites a cuánto pueden cambiar el grafo los insplits y los outsplits, por lo que podemos describir exactamente cuándo dos grafos meteóricos son SSE”, detalla. “Por otra parte, sabemos que dos grafos son SE si y sólo se cumple cierta afirmación sobre objetos algebraicos – si sus «monoides talentosos» son isomorfos graduados–, que puede calcularse a partir de las matrices de adyacencia de los grafos. Lo que demostramos es que este isomorfismo de monoides talentosos se produce precisamente cuando los grafos meteóricos son SSE”, añade.

Ahora, la investigadora espera que la estrategia de demostración usada para los grafos de meteóricos permita verificar que SE es equivalente a SSE para más clases de grafos (o, equivalentemente, desplazamientos de tipo finito).