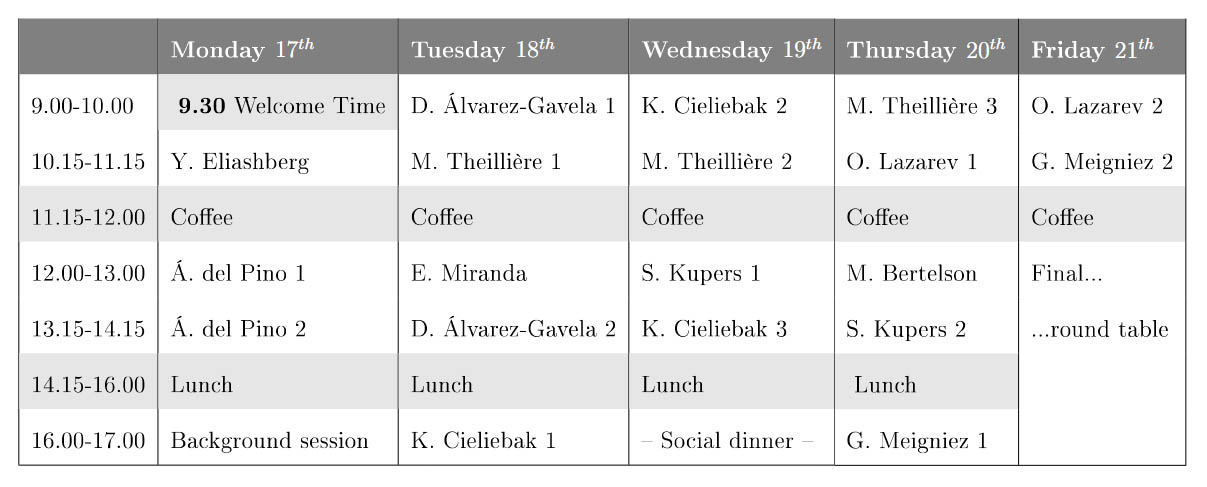
Schedule

Titles

Monday

Y. Eliashberg. Flexible and Rigid facets of Mathematics
Á. del Pino Gómez. Preliminaries I
Á. del Pino Gómez. Preliminaries II

Tuesday

D. Álvarez-Gavela. The holonomic approximation lemma I
M. Theillière. Convex integration in 1 dimension
E. Miranda. The h-principle and Reeb/Beltrami embeddings
D. Álvarez-Gavela. The holonomic approximation lemma II
K. Cieliebak. The h-principle for wrinkled submersions

Wednesday

K. Cieliebak. The h-principle for wrinkled embeddings
M. Theillière. Theory of convex integration
S. Kupers. Delooping and h-principles I
K. Cieliebak. Igusa's theorems on generalized Morse functions

Thursday

M. Theillière. Convex integration and the Nash-Kuiper theorem
O. Lazarev. Background on Weinstein domains and connections to Legendrian knot theory
M. Bertelson. Discretizing symplectic topology
S. Kupers. Delooping and h-principles II
G. Meigniez. The h-principle in the homotopy theory of foliations (part 1)

Friday

O. Lazarev. Simplifying (and complicating) Weinstein presentations
G. Meigniez. The h-principle in the homotopy theory of foliations (part 2)