PARA DOCENTES 2012

Matemáticas en la naturaleza

“El matemático juega a un juego en el que él mismo inventa las reglas, mientras que el físico juega a un juego en el que las reglas son proporcionadas por la naturaleza; pero a medida que pasa el tiempo se hace cada vez más evidente que las reglas que el matemático encuentra interesantes son las mismas que las que ha escogido la naturaleza”

- Paul Adrien Maurice Dirac, físico teórico inglés

Algunas veces la propia naturaleza inspira a los matemáticos en sus definiciones y desarrollos. Por ejemplo, las ecuaciones diferenciales fueron inicialmente tratadas por Newton para estudiar el movimiento planetario.  Su estudio continuó a medida que se afianzó su utilidad en las ciencias naturales, especialmente en la física,  con problemas importantes como la ley del movimiento de Newton, las ecuaciones de Euler para la hidrodinámica, la ecuación de calor por Fourier, etc. 

Pero también sucede de manera opuesta: de repente, por sorpresa se observa en la naturaleza una construcción matemática ideada de manera abstracta en el pensamiento de un investigador. Así sucede con sucesión de Fibonacci, o con las simetrías de las plantas.

El objetivo de este concurso es invitar a los participantes  a que encuentren por sí mismos estas correlaciones entre los conceptos matemáticos y los objetos del mundo natural y que, una vez identificados, hagan representaciones de los mismos a través del arte urbano.

Para servir de inspiración y como apoyo a esta búsqueda propia de las matemática de la naturaleza, se dan los siguientes ejemplos ilustrativos:

FRACTALIDAD

Definición

Un fractal es un objeto geométrico cuya estructura básica se repite en diferentes escalas, hasta el infinito.

La forma más sencilla de entenderlo es con un dibujo:

La idea es que, observando el objeto en cualquier escala, vemos básicamente lo mismo. Como cuando miramos un helecho de cerca: sus ramas parecen de nuevo helechos más pequeños, y las hojas vuelven a reproducir esta estructura.

Fractales naturales

Hay determinados objetos de la naturaleza que se pueden representar (simbólicamente, utilizando estructuras geométricas) mediante fractales matemáticos de manera bastante precisa.

Esto sucede, por ejemplo, en la línea de la costa. Si miramos con detalle, podemos ver granitos de arena que se ordenan formado una estructura granulada de entrantes y salientes. Si nos fijamos en la playa, la erosión de las olas produce una estructura similar. Si miramos toda una zona de cosa, cada una de las playas se convierte en un entrante y de manera global se observa la misma estructura.

También las nubes, las montañas, el sistema circulatorio o los copos de nieve son fractales naturales.

Romanescu (Brassica oleracea)

Pese a que parezca una estructura muy enrevesada, la fractalidad es muy habitual en la naturaleza. De hecho, resulta muy práctica: repetir la estructura ilimitadamente es una forma muy útil de aumentar la superficie (sin tener que aumentar demasiado el volumen)

Nuestros órganos, como por ejemplo los pulmones, son fractales.

Definición matemática

Esta complejidad no es fácil de delimitar, y tampoco de describir con matemáticas, como sí se puede hacer con las ecuaciones de una figura regular. La verdad es que el concepto de fractal no dispone de una definición matemática precisa y de aceptación general. Varios matemáticos, como B. Mandelbrot o  D. Sullivan intentaron dar una definición pero sus resultados no fueron capaces de plasmar totalmente el resultado.

Los fractales naturales, como las hojas o las grietas, se diferencian de los fractales matemáticos en que son aproximados, es decir, la estructura que se repite no es exactamente la misma –aunque sí sea muy parecida- y su autosimilaridad se extiende solo a un rango de escalas es decir, no se repite hasta el infinito.

Características

Ante la dificultad de dar una definición matemática exacta los fractales se definen por las propiedades que cumplen. Un objeto geométrico fractal tiene las siguientes características:

· Es demasiado irregular para ser descrito en términos geométricos tradicionales.

· Es autosimilar, es decir, su forma está hecha de copias más pequeñas de la misma figura.

No basta con una sola de estas características para definir un fractal. Por ejemplo, la recta real no se considera un fractal, pues a pesar de ser un objeto autosimilar puede describirse en términos geométricos tradicionales.

Nuestros órganos, como por ejemplo los pulmones, son fractales.

Origen del concepto

En el siglo XVII, el filósofo Gottfried Leibnitz jugueteó con el concepto de la autorepetición recursiva. Según esta idea, el universo podría estar formado por unas unidades llamadas mónadas, cada una de las cuales contenía en sí misma, a su vez, todo el universo, y así sucesivamente. Comparaba el cosmos con un jardín que tuviera un estanque lleno de peces, pero en el que cada hoja, cada piedra y cada escama de cada pez fuera, a su vez, un jardín completo, repitiéndose hasta el infinito más allá́ de nuestra vista.

La perfección, en este contexto, era un universo que se contemplaba a sí mismo desde todos los puntos de vista posibles. Después de él, un buen número de matemáticos comenzaron a juguetear con formulas que, repetidas hasta el infinito tenían curiosísimas propiedades.

Esta idea de repetición a distintos niveles fue recuperada durante el siglo XX y aplicada a distintos ámbitos de la naturaleza, descubriéndose que realmente existía en los ámbitos más diversos, formando lo que se conoce como estructuras fractales.”

- Guillermo Santamaría. “Fractales… ¡qué arte!”. Redes.

Primeros fractales matemáticos

En 1872 Weierstrass, mientras buscaba un ejemplo de función continua pero no derivable en ningún punto dio con la llamada ‘función de Weirestrass’, cuyo grafo hoy en día consideraríamos fractal:

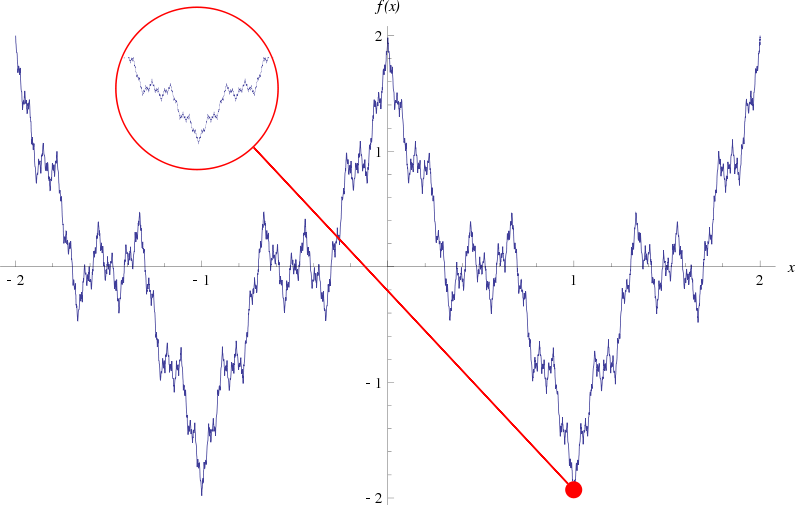Posteriormente aparecieron ejemplos con propiedades similares pero una definición más geométrica. Estos ejemplos se construyen partiendo de una figura inicial (semilla), a la que se aplican una serie de construcciones geométricas sencillas. La serie de figuras obtenidas se va aproximando a una figura límite que corresponde al que hoy llamamos conjunto fractal.

Así, en 1904, Helge von Koch definió una curva con propiedades similares a la de Weierstrass: el copo de nieve de Koch. En 1915, Waclaw Sierpinski construyó su triángulo y, un año después, su alfombra.

Construcción del triángulo de Sierpinski:

Estos conjuntos mostraban las limitaciones del análisis clásico, pero eran vistos como objetos artificiales. Pocos matemáticos vieron la necesidad de estudiar estos objetos en sí mismos. Henri Poincaré los denominó "galería de monstruos”.

En 1919 surgió una herramienta básica en la descripción y medida de estos conjuntos: la dimensión fractal o de de Hausdorff-Besicovitch. Para que nos hagamos una idea, el concepto de dimensión define los grados de libertad con los que nos podemos mover en un espacio. Una recta tiene dimensión uno, porque solo podemos avanzar y retroceder en una dirección, la de la recta. El plano tiene dimensión dos, ya que podemos movernos a lo largo y a lo ancho, El copo de Koch tiene dimensión fractal aproximadamente 1.26186 ln(4)/ln(3) ), y del triángulo de Sierpinski, aproximadamente. 1.585 ( ln(3)/ln(2) ), logaritmos neperianos

En el siglo XX volvieron a llamar la atención de los científicos y en particular, de uno de las mentes más revolucionarias del siglo: Benoît Mandelbrot.

Benoît Mandelbrot

El padre de la geometría fractal

Benoît Mandelbrot nació en Varsovia (Polonia) en 1924 pero la Segunda Guerra Mundial le obligó a refugiarse en Francia. Allí, en París, obtuvo su doctorado y poco después partió a EE UU donde realizó de estancias en el MIT y en Princeton. Después trabajó para los laboratorios IBM research y fue profesor en la Universidad de Yale (EE. UU.).

En 1961 Madelbrot quiso estudiar una de las grandes preocupaciones de los economistas del momento: las fluctuaciones en los precios del algodón. Recogiendo los datos del comportamiento del precio del algodón de los últimos 100 años construyó las primeras funciones fractales.

En 1970 publicó ¿Cuánto mide la costa de Gran Bretaña?, un artículo en el que daba la solución a esta pregunta mediante los fractales.

Mandelbrot abrió el camino hacia la comprensión de una nueva rama de las matemáticas que no llegó hasta bien entrados los años noventa del siglo pasado. Tuvo la perseverancia necesaria para continuar con unas investigaciones completamente alejadas de lo que se estaba estudiando en ese momento que, años después, resultaron tremendamente útiles.

Aplicaciones

Entrado ya el siglo XXI, ha quedado más que demostrada su utilidad en aplicaciones como la comprensión de datos, modelado de formas naturales, sistemas dinámicos o en el arte.

• Compresión de imágenes

Comprimir la imagen de un objeto autosemejante es relativamente sencillo: debemos encontrar un conjunto de transformaciones que lleva la figura completa en cada una de sus partes autosemejantes. La información sobre la imagen quedará codificada en el conjunto de transformaciones, y la aplicación reiterada de dichas transformaciones permitirá obtener la imagen procesada en cuestión.

Pero con muchas imágenes reales no funciona este enfoque: la imagen de un gato no presenta pequeños gatitos distorsionados sobre sí mismo. Aun así, para poder aplicar un método parecido, en 1989 Arnaud Jacquin creó un esquema en el la imagen se subdivide mediante una partición y para cada región resultante se busca otra región similar a la primera bajo las transformaciones apropiadas.

Es un sistema de compresión con pérdidas, y aún se tarda mucho en encontrar las transformaciones que definen la imagen. No obstante, una vez encontradas, la descodificación es muy rápida.

• Modelado de formas naturales

Las formas fractales están presentes en la materia biológica como formas sofisticadas en el desarrollo evolutivo de la materia biológica. Se presentan en procesos en los que se producen saltos cualitativos en las formas biológicas, es decir posibilitan catástrofes (hechos extraordinarios) que dan lugar a nuevas realidades más complejas.

De esta manera, las hojas son morfológicamente similares a la pequeña rama de la que forman parte que, a su vez es similar a la forma del árbol, y sin embargo cualitativamente no es lo mismo una hoja (forma biológica simple), que una rama o un árbol (forma biológica compleja).

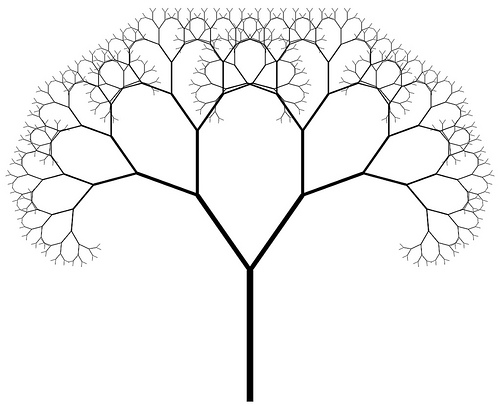• En manifestaciones artísticas

Los fractales se han usado tanto en la composición armónica y rítmica de una melodía como en la síntesis de sonidos.

Con programas informáticos como Apophysis o Ultra Fractal se pueden hacer imágenes con técnicas diversas; cambiando parámetros, geometría de triángulos o con transformaciones aleatorias (a veces llamadas "mutaciones").

La literatura también tiene sus ejemplos de fractalidad. Sin duda, el maestro fue Jorge Luis Borges, con relatos como El jardín de los senderos que se bifurcan, El Aleph o la Biblioteca de Babel. También incluyeron conceptos fractales  Nabokov, en El ojo, y Arthur C. Clarke, en El espectro del Titanic.

Otro ejemplo se encuentra en el comienzo de Secuencias, un microrrelato de Julio Cortázar publicado dentro de Papeles inesperados:

“Dejó de leer el relato en el punto donde un personaje dejaba de leer el relato...”.

SUCESIONES

Definición

Una sucesión es una lista ordenada de objetos (denominados términos, elementos o miembros).

A diferencia de un conjunto, el orden en que aparecen los términos es relevante y un mismo término puede aparecer en más de una posición.

En algunos casos este tipo de listas ordenadas aparecen en la naturaleza. Uno de los ejemplos más famosos es la sucesión de Fibonacci.

La sucesión de Fibonacci

La sucesión de Fibonacci es una sucesión infinita de números naturales en la que cada término es la suma de los dos anteriores definiendo el primer (f1= 0) y segundo término (f2=1): 0,1,1,2,3,5,8,13…

También es conocida como la secuencia áurea, ya que a los renacentistas les parecía algo divino que albergaba las relaciones (proporciones) de la perfección.

Fue descrita en Europa por Leonardo de Pisa, matemático italiano del siglo XIII también conocido como Fibonacci. Él la enunció como solución a un problema de cría de conejos:

"Cierto hombre tenía una pareja de conejos juntos en un lugar cerrado y uno desea saber cuántos son creados a partir de este par en un año cuando es su naturaleza parir otro par en un simple mes, y en el segundo mes los nacidos parir también"

Sucesión en las flores y las abejas

La sucesión tiene numerosas aplicaciones en ciencias de la computación, matemáticas y teoría de juegos, pero además aparece en configuraciones biológicas, como por ejemplo en las ramas de los árboles, en la disposición de las hojas en el tallo y en la flor de la alcachofa.

El número de espirales en numerosas flores y frutos también se ajusta a parejas consecutivas de términos de esta sucesión: los girasoles tienen 55 espirales en un sentido y 89 en el otro, o bien 89 y 144.

Las margaritas presentan las semillas en forma de 21 y 34 espirales. Y cualquier variedad de piña presenta siempre un número de espirales que coincide con dos términos de la sucesión de los números de Fibonacci, 8 y 13; o 5 y 8.

También aparece en el mundo animal, por ejemplo, los machos de una colmena de abejas tienen un árbol genealógico que cumple con esta sucesión. El hecho es que un zángano (1), el macho de la abeja, no tiene padre, pero sí que tiene una madre (1, 1), dos abuelos, que son los padres de la reina (1, 1, 2), tres bisabuelos, ya que el padre de la reina no tiene padre (1, 1, 2, 3), cinco tatarabuelos (1, 1, 2, 3, 5), ocho trastatarabuelos (1, 1, 2, 3, 5, 8) y así sucesivamente, cumpliendo con la sucesión de Fibonacci.

Simetría

Definición

La simetría es una característica de formas geométricas, sistemas, ecuaciones y otros objetos materiales y entidades abstractas, relacionada con su invariancia bajo ciertas transformaciones, movimientos o intercambios.

Un ejemplo sencillo es la simetría axial, es decir, alrededor de un eje, como el que presenta el cuerpo humano, una hoja, cualquier polígono regular o la imagen a uno y otro lado del espejo.

La simetría se observa en muchos organismos vivos.  De hecho, se puede decir que es una propiedad distintiva de la naturaleza. A simple vista podemos observarla en las flores y en los animales.

También, aunque esta no podamos verla, está presente en fenómenos cuánticos del mundo atómico y subatómico. De hecho, muchos científicos afirman que la física moderna, desde lo más pequeño a lo más grande, es decir, desde los átomos, los quarks o los núcleos, pasando por lo molecular en estado sólido, hasta la estructura misma del universo, requiere del concepto de simetría para su comprensión.

Simetría de los seres vivos

En biología la simetría corresponde a una distribución equilibrada en el cuerpo de los organismos de aquellas partes que aparecen duplicadas.  Por ejemplo, los seres humanos son simétricos respecto a un eje vertical que divide nuestro cuerpo en la dirección de la columna vertebral: tenemos dos brazos, dos piernas, dos ojos, dos orejas… simétricos respecto a esta recta.

Los planes corporales de la mayoría de organismos pluricelulares exhiben alguna forma de simetría, bien sea simetría radial (definida por un eje distinto en sus dos extremos) o simetría bilateral. Una pequeña minoría no presenta ningún tipo de simetría (son asimétricos).

La mayoría de especies animales tiene simetría bilateral, aunque hay especies como los erizos y las estrellas de mar que presentan simetría radial secundaria. La simetría bilateral permite la definición de un eje corporal en la dirección del movimiento, lo que favorece la formación de un sistema nervioso centralizado y la cefalización.

Número áureo

Definición

El número áureo o de oro es un número irracional con valor aproximado:

1,618033988749894848204586834365638117720309...

El número áureo surge de la división en dos de un segmento ab guardando las siguientes proporciones: La longitud total a+b es al segmento más largo a, como a es al segmento más corto b.

Se suele representa con la letra griega φ (fi), en honor al escultor griego Fidias.

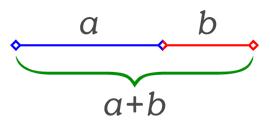Es decir, (a+b):a= a:b

Propiedades

Es un número irracional (decimal infinito no periódico) que posee muchas propiedades interesantes.

Puede expresarse como fracciones continuas:

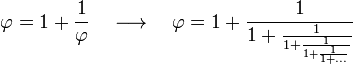También se puede expresar como una serie de raíces anidadas:

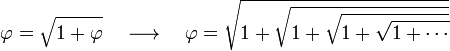Además, el número áureo alberga una proporción considerada, en muchas ocasiones, ‘perfecta’. De hecho, surgió en la antigüedad como una relación o proporción entre segmentos de rectas,  no como unidad.

Proporción áurea

Esta relación se encuentra tanto en algunas figuras geométricas como en la naturaleza, por ejemplo en las nervaduras de las hojas de algunos árboles, en el grosor de las ramas, en el caparazón de un caracol y en los flósculos de los girasoles.

Asimismo, se atribuye un carácter estético a los objetos cuyas medidas guardan la proporción áurea. A lo largo de la historia, se ha atribuido su inclusión en el diseño de diversas obras de arquitectura y otras artes, aunque algunos de estos casos han sido cuestionados por los estudiosos de las matemáticas y el arte.

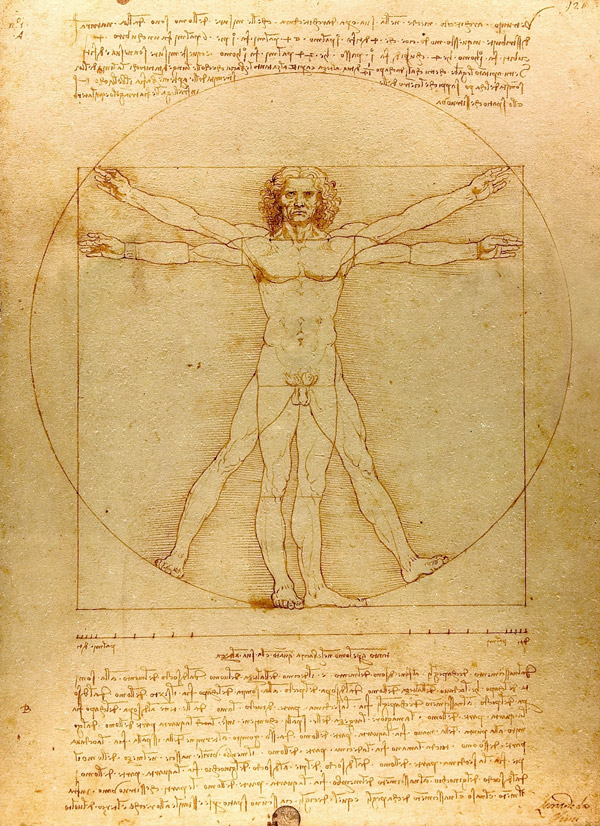La representación del Hombre de Vitruvio de Leonardo da Vinci utiliza el sistema fraccionario propuesto por Vitruvio y no el  número áureo como comúnmente se cree.

Relación con la serie de Fibonacci, con los pentágonos regulares y con las espirales

El número de oro también está relacionado con la serie de Fibonacci, de la que ya hemos hablado. Si consideramos el cociente del enésimo número de Fibonacci (Fn), y el siguiente número de Fibonacci, (Fn + 1), descubrimos que, a medida que n aumenta, este resultado oscila, y es alternativamente menor y mayor que la razón áurea.

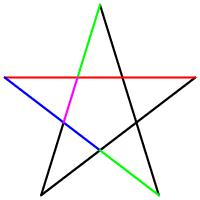Por otro lado, el número áureo tiene un papel muy importante en los pentágonos regulares y en los pentagramas. Cada intersección de partes de un segmento interseca a otro segmento en una razón áurea. Dentro del pentagrama, sus triángulos y los polígonos inscritos se pueden observar más relaciones áureas.

Además hay espirales que también siguen proporciones áureas.

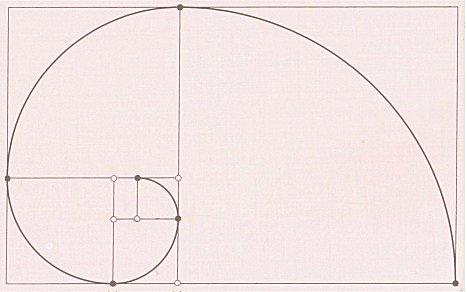‘Espiral de Durero’, construcción del pintor renacentista Alberto Durero (1471-1528) en su obra "Instrucción sobre la medida con regla y compás de figuras planas y sólidas".

El número áureo en la naturaleza

El número áureo aparece en numerosas propiedades o características de las plantas. El papel del número áureo en la botánica recibe el nombre de Ley de Ludwig y determina, por ejemplo, la disposición de los pétalos de las flores y la distribución de las hojas en un tallo.

La relación entre las nervaduras de las hojas de los árboles, la relación entre el grosor de las ramas principales y el tronco y la relación entre las ramas principales y las secundarias también obedecen a la razón aurea.

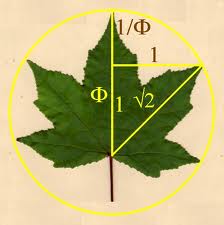También se observa en la cantidad de espirales de una piña (ocho y trece espirales), flores o inflorescencias.

Creación de patrones

Definición

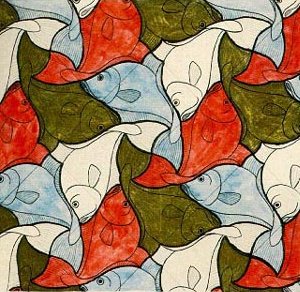
Un patrón es un objeto recurrente, como por ejemplo el dibujo de un estampado o un mosaico.

Estos elementos se repiten de una manera predecible. Pueden  generarse a partir de una plantilla o un modelo.

Los patrones más básicos, llamados teselaciones, se basan en la repetición y la periodicidad. Una única plantilla, azulejo o célula, se combina mediante duplicados sin cambios o modificaciones.

Patrones de la naturaleza

En la naturaleza se pueden encontrar diversos paisajes, estructuras y pelajes de animales dispuestos de manera similar a un patrón matemático.

Por ejemplo, las manchas de un leopardo parecen seguir un modelo que define el dibujo, no es una disposición caótica. O también en los movimientos de determinados grupos de animales se pueden observar patrones distinguibles por el ojo humano.

El origen de estos patrones es, en muchos casos, desconocido. Aunque algunas veces tiene una explicación geológica o química, como es el caso de las rayas de los mamíferos.

El genial matemático inglés Alan Turing, padre de la computación moderna, propuso en la década de 1950 una idea sobre la formación de algunos patrones biológicos, como las rayas del tigre o las manchas del leopardo. Según Turing, estas repetición de patrones está generada por un par de unos productos químicos llamados morfógenos que trabajan juntos como un “activador” y un “inhibidor”.

Este mismo año 2012 investigadores del King’s College de Londres han encontrado la primera prueba que confirma la teoría de Turing .