IDEAS BÁSICAS

Qué son los fluidos

Los fluidos son materia en estado líquido, gaseoso y plasma.

Por ejemplo, El agua y la atmósfera son fluidos, sin los cuales no existiría la vida tal y como la conocemos. También son fluidos determinadas partes del interior de la tierra o las nubes de azufre que emite un volcán en erupción.

* La atmósfera terrestre es un fluido. Fotografía tomada desde la Estación Espacial internacional.  

* El magma de los volcanes también es materia fluida.
Autor: Adrien Cretin en Flickr.

La forma de los líquidos la da el recipiente que los aloja, y los gases directamente no tienen forma propia.

* El líquido toma la forma del recipiente que lo aloja.

* Los gases carecen de forma definida. Autor: NDomer73 en Flickr

Estudios de los fluidos

La mecánica de fluidos es un campo de la física muy amplio que estudia el movimiento y la estructura de los fluidos y las fuerzas que los provocan. También estudia las interacciones entre el fluido y el contorno que lo limita. Las matemáticas son el lenguaje que se emplea para describir estos fenómenos.

¿De dónde salen las ecuaciones de los fluidos?

Las ecuaciones se obtienen al aplicar ciertos principios que sabemos que se cumplen al volumen fluido. Asumimos que los fluidos verifican la ley de la conservación de la masa y de conservación de la cantidad de movimiento y otras leyes.

Sin embargo, la descripción de los fluidos “reales” implica modelos matemáticos muy complicados, que aun hoy, con el desarrollo computacional actual, son difíciles de tratar. Por ello, ya en el s. XVIII, los matemáticos Bernoulli y Euler buscaron maneras de simplificar el problema, asumiendo ciertas condiciones razonables: (1) considerar fluidos incompresibles (que no pueden comprimirse) y (2) considerar fluidos perfectos (sin viscosidad).

* El agua es un fluido casi incompresible ya que tiene la capacidad de oponerse a la compresión. Autor: Downtowngal.

* Los gases, sin embargo, son fluidos compresibles. Autor: தகவலுழவன்

La viscosidad es característica de todos los fluidos, tanto líquidos como gases, si bien, en este último caso su efecto suele ser despreciable, están más cerca de ser fluidos ideales.

* La sustancia del fondo tiene una viscosidad más alta que la el líquido claro que está encima. Autor: Anynobody.

Sin embargo, la simplificación de los fluidos de Euler conlleva ciertas desventajas. Por ejemplo, no admiten arrastre lateral, y según este modelo, aunque un barco flotaría en agua, los aviones no volarían. Por tanto, fue necesario buscar un modelo de “nivel superior”. Cauchy, Navier y Stokes consideraron fluidos más realistas que sí incluyen los efectos de la viscosidad y de esta manera se obtienen las ecuaciones de Navier-Stokes , que dan el marco teórico completo de la disciplina.

Fue en 1822 y 1845, cuando los matemáticos Claude-Louis Navier y Gabriel Stokes perfeccionaron la fórmula de Euler al tener en cuenta el grado de viscosidad de los fluidos a estudiar.

* Busto del Claude Louis Marie Henri Navier en la École Nationale des Ponts et Chaussées.

*Sir George Gabriel Stokes.

Ecuaciones de Navier- Stokes

Las ecuaciones de Navier-Stokes describen el movimiento de los fluidos “reales” y su profundo entendimiento es uno de los grandes retos matemáticos de este milenio. Conocer sus soluciones permitiría predecir el comportamiento de la atmósfera, de las corrientes oceánicas, del magma terrestre…

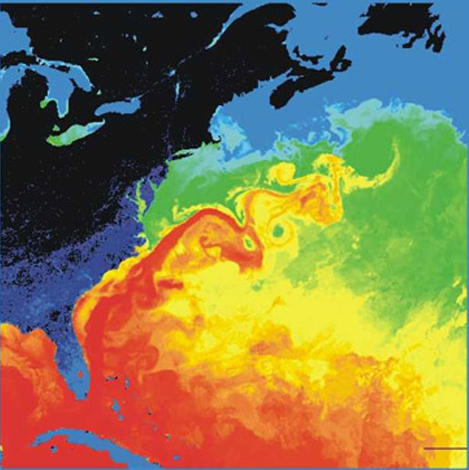
* Golfstrom.

* Una imagen de satélite de la costa de California, mostrando la falta de nubes en la zona costera debido al ascenso de aguas frías que corresponden a lo que se llama emersión de aguas profundas por el movimiento de rotación terrestre. Dicha carencia de nubes identifica a esta corriente.

A lo largo de la historia los seres humanos han sido capaces de crear teorías que permiten anticiparse a lo que va a pasar en la naturaleza en el futuro, una vez que se tiene suficiente información sobre el presente: el movimiento de los astros, el lanzamiento de una pelota, el giro de una peonza… La mayoría de estas teorías utilizan las matemáticas como lenguaje.

* Trayectoria parabólica del agua. El agua de esta fuente recorre una parábola. Autor: GuidoB.

Pensemos ahora en un río, una masa de agua moviéndose de manera que a cada punto, a cada gota que lo forma, podemos asociarle una velocidad (consideremos que es un vector que indica la rapidez y la dirección con la que se mueve). Si conocemos la velocidad de cada gota en un instante de tiempo, en el presente, ¿podemos decir cual va ser su velocidad en el futuro?

* Río St. Francis en el área de Silver Mines del Bosque Nacional Mark Twain en Missouri. Autor: Kbh3rd

Los matemáticos y los físicos han sido capaces de encontrar una ecuación que se puede aplicar a todos estos casos pero es tan complicada que a menudo resulta imposible encontrar sus soluciones y, por lo tanto, leer el futuro en ellas. Hablamos de la ecuación de Navier-Stokes.

Y, ¿en qué consisten estas ecuaciones? La base en la que se sustentan es fácil de entender. Partimos de tres leyes físicas:

• La ley de la conservación de la masa.
• La segunda ley de Newton (Ley de conservación del movimiento).
• Una ley de estado que relaciona la presión con la densidad

Estas tres condiciones físicas se pueden traducir a un lenguaje matemático a través de unos objetos que se conocen como ecuaciones en derivadas parciales. Las soluciones de estas ecuaciones  nos dicen como varia con el tiempo la densidad, la velocidad y la presión del fluido en cada punto del espacio en el que yace. Su complejidad es tal, que hasta ahora, se tiene muy poca información sobre su comportamiento y su comprensión forma parte de uno de los siete problemas del milenio.

La complejidad que entraña interpretar la información codificada en estas soluciones, y la utilidad que tendría el conseguirlo, hacen que se lleve a cabo una intensa investigación en matemáticas en el campo de las ecuaciones de los fluidos. En él, los matemáticos intentan desarrollar técnicas y métodos que nos permitan entender aquello que sabemos que está recogido en las ecuaciones.

Conseguirlo nos permitirá confiar en las predicciones meteorológicas, entender cómo y por qué se forman los huracanes, cómo se mueve un tsunami y  muchas otras aplicaciones a la ingeniería. Pero también sería un logro intelectual enorme por sí mismo. Avanzar en el entendimiento de estas ecuaciones implicaría disponer de unas matemáticas aún más potentes, y esto transciende más allá de los propios  fluidos.

Un problema de un millón de dólares

* La Fundación Clay es una institución privada dedicada a promover la investigación matemática.

Las ecuaciones de Navier-Stokes son uno de los denominados problemas del milenio, siete problemas matemáticos seleccionados en el año 2000 por el Instituto Clay de Matemáticas por su especial complejidad y cuya solución será premiada con un millón de dólares. Hasta el momento, solo uno de los siete problemas, la Conjetura de Poincaré, ha sido resuelto.

Con esta selección el Instituto Clay quiso emular un siglo después los Problemas de Hilbert, enunciados por el famoso matemático David Hilbert en 1900 y cuyo tratamiento y resolución dieron un gran impulso a las matemáticas del siglo XX.

* David Hilbert (1862, Königsberg; 1943, Göttingen)

La relevancia de estos problemas viene de todo el desarrollo teórico que tienen detrás. El problema en sí implica la creación de técnicas y procedimientos que suponen un gran avance en sus respectivos campos

Aplicaciones de la Mecánica de Fluidos

Pese a que todavía hay muchas preguntas abiertas, la Mecánica de Fluidos permite comprender el medio continuo y sus ecuaciones sirven para diseñar modelos de sistemas complejos como la atmósfera o el mar. Gracias a estos modelos, cada vez más precisos, es posible:

- Predecir el tiempo atmosférico.

- Comprender la naturaleza de los vientos,

- Entender la naturaleza de los movimientos del mar, olas, mareas y corrientes.

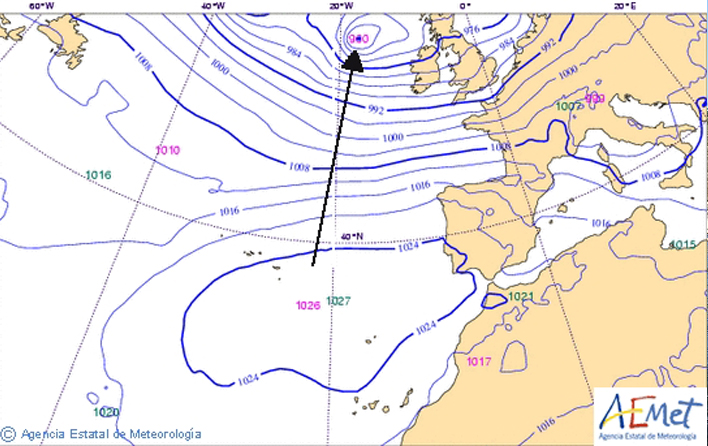
* Mapa de isobaras. Autor: Simon Eugster .

Además, el lenguaje matemático permite plantear y resolver los problemas de la hidráulica tradicional: tuberías, canales...

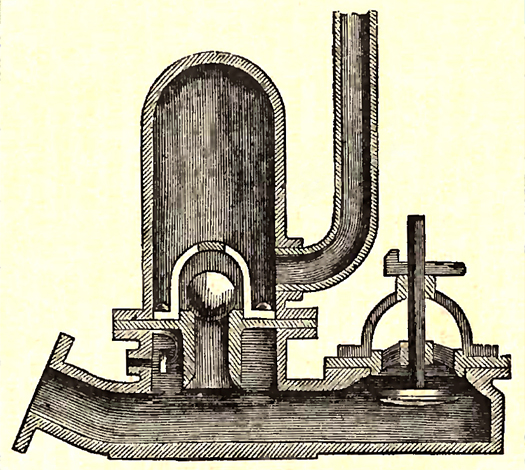
* Cilindro hidráulico.

Ya desde finales del siglo XIX, la náutica y la naciente aeronáutica fomentan la investigación en el cálculo del vuelo de objetos.

* Aeronatica Caproni di Predappio.

Matemáticas de los fenómenos de la naturaleza

La hidrodinámica es un campo inmenso de interés para los matemáticos, pero también para los físicos, los ingenieros y los meteorólogos. En muchos fenómenos de la naturaleza se han originado modelos o sistemas de ecuaciones, que atañen a los fluidos y que, de alguna manera, se derivan de las leyes fundamentales de los mismos. He aquí una pequeña muestra de fenómenos que se pueden observar a través de la potente lente de las matemáticas:

Frentes de aire frio y aire caliente

De las ecuaciones de Navier-Stokes se deducen ecuaciones que sirven para construir modelos de evolución de los frentes atmosféricos.

* Frente frío aproximándose a Cook Strait (Nueva Zelanda). Author: Phillip Capper.

Torbellinos

A menudo los fluidos desarrollan estructuras en forma de torbellinos, también conocidos como vórtices, que son capaces de concentrar una gran cantidad de energía en una región pequeña del espacio, y que poseen una gran capacidad destructiva. Estos vórtices pueden subsistir por largos períodos de tiempo y desplazarse en el espacio, como hacen los huracanes y los tornados. Estudiar la evolución de estas soluciones de las ecuaciones de los fluidos y demostrar matemáticamente sus propiedades es una tarea muy interesante.

* Huracán Irene.

* Tornado en Oklahoma City  (EE. UU.)

Gotas

Por qué son las gotas esféricas? La razón está en la tendencia de su superficie a ocupar la mínima área posible, y da lugar a fenómenos muy interesantes de cambio de forma. Un ejemplo es un chorro de agua que rompe en un conjunto de puntos desconectados entre sí, dando lugar a gotas. Pero también resulta interesante el fenómeno contrario (por ejemplo, el chapapote), cuando un líquido viscoso dentro de otro que lo sea menos, puede desarrollar filamentos que llegan casi al tamaño molecular.

* Gota de agua. Autor: José Manuel Suárez. Fuente: Flickr
http://commons.wikimedia.org/wiki/File:Water_drop_001.jpg

* Gotas de rocío. Autor: Steve took it

Ondas: Olas

¿Qué son las olas? Se trata de soluciones en forma de onda para las ecuaciones de Euler o Navier-Stokes, análogas a las soluciones en forma de onda para el electromagnetismo (ondas de radio o de televisión). Estas ondas pueden tener longitudes del orden de centímetros -como son las llamadas capilares-, o tener longitudes kilométricas -como los devastadores tsunamis-. Pueden también aparecer, bajo ciertas circunstancias, en algunos tipos de nubes. Todas ellas presentan problemas matemáticos que son fascinantes y e interesantes de investigar.

La gran ola de Kanagawa.

Medios porosos

¿Cómo cambia la dinámica de un fluido en un medio poroso? ¿Cómo se mueven las aguas subterráneas? El ingeniero Henry Darcy, en 1856, dedujo de forma experimental que el fluido se rige por lo que hoy en día se conoce como la ley de Darcy-

El agua subterránea es el medio de transporte de los químicos disueltos y de los contaminantes. Los materiales disueltos de los desechos acumulados en el suelo o en enterrados pueden ser transportados desde el lugar del depósito por el flujo del agua subterránea contaminada, por lo que el estudio del transporte del fluido en medios porosos es muy importante para entender y prevenir la dispersión de contaminantes.

* Río subterráneo en la cueva de Wookey Hole Cave and underground river. Imagen: Becks.

Investigación hoy

La mecánica de fluidos es un campo de estudio muy activo. A pesar de la importancia práctica de sus problemas y de los esfuerzos de muchos grandes matemáticos durante varios siglos, como ya hemos visto, quedan todavía algunas cuestiones fundamentales en la mecánica de fluidos que esperan respuesta.

Esta disciplina está en la frontera entre el análisis matemático, las simulaciones numéricas y la física de los medios continuos, pero además tiene una estrecha relación con otras ciencias: especialmente con la física, pero también con la ingeniería, o la meteorología.

En el Instituto de Ciencias Matemáticas (ICMAT) esta rama es una de las más fructíferas y en los últimos años han obtenidos importantes resultados, como: la descripción matemática de cómo se produce la ruptura de una ola, obtenida por el equipo de Diego Córdoba, y la resolución de la conjetura de Arnold por Daniel Peralta y Alberto Enciso.

* Ruptura de una gran ola en Santa Cruz (California, EE. UU.) Autor: Brocken Inaglory.

Historia de la mecánica de fluidos.

El ser humano, a lo largo de su historia, ha aprendido a comprender, e incluso predecir, el comportamiento de los fluidos y a crear tecnología relacionada con los mismos, como las tuberías, los canales y los aviones.

Los orígenes de esta disciplina se remontan al nacimiento de la agricultura. Estas primeras sociedades necesitaban sistemas de regadíos y canales y empezaron a crear y acumular conocimientos sobre el agua. También el auge de la navegación fomentó el interés en este tipo de estudios. En la Antigüedad Clásica vivió, como muchas otras áreas de la matemática y de la física, una etapa de esplendor en la que destacan personajes como Arquímedes.

Arquímedes

Arquímedes de Siracusa (Siracusa (Sicilia), 287 a. C. –212 a. C.) fue uno de los grandes matemáticos de todos los tiempos. Como muchos otros sabios griegos no se limitó a una sola disciplina sino que también hizo contribuciones a la física, ingeniería, y astronomía. Propuso los fundamentos de hidrostática que marcan el origen del estudio científico de los fluidos.

* Arquímedes de Siracusa (Siracusa (Sicilia), 287 a. C. –212 a. C.)

Una de las anécdotas más conocidas sobre Arquímedes narra su invención de un método para determinar el volumen de un objeto con una forma irregular. Cuando Arquímedes, durante el baño, dio con la solución, se dice que salió corriendo desnudo por las calles, gritando "¡Eureka!" (en griego antiguo: "εὕρηκα" que significa "¡Lo he encontrado!"), tan emocionado que olvidó vestirse.

* ¡Eureka! Dominio público.

Isaac Newton (1643 - 1727) fue un físico, filósofo, teólogo, inventor, alquimista y matemático inglés, autor de los Philosophiae naturalis principia mathematica, más conocidos como los Principia, uno de los tratados más importantes de la historia de la ciencia, que establece las bases de la mecánica clásica. Entre muchos otros logros científicos, desarrolló el cálculo matemático.

La contribución de Newton al estudio de los fluidos fue múltiple y a niveles muy diferentes. Abarcó desde sus fundamentos, en forma indirecta, hasta los meticulosos experimentos que llevó a cabo sobre vórtices (remolinos) y viscosidad (fricción interna).

* Retrato de Sir Isaac Newton por el pintor Gottfried Kniller.

Desde el punto de vista general, el marco teórico, el aparato matemático y las leyes físicas que Newton estableció, fueron, y siguen siendo, los ingredientes esenciales de la teoría de los fluidos. Estos elementos fueron una aporte fundamental, aunque indirecto, para el establecimiento final de la teoría que realizó la notable generación que le siguió, formada por Euler, dos de los Bernoulli, D'Alambert y Lagrange.

* Retrato de Leonhard Euler (1707-1783) por el pintor Jakob Emanuel Handmann.