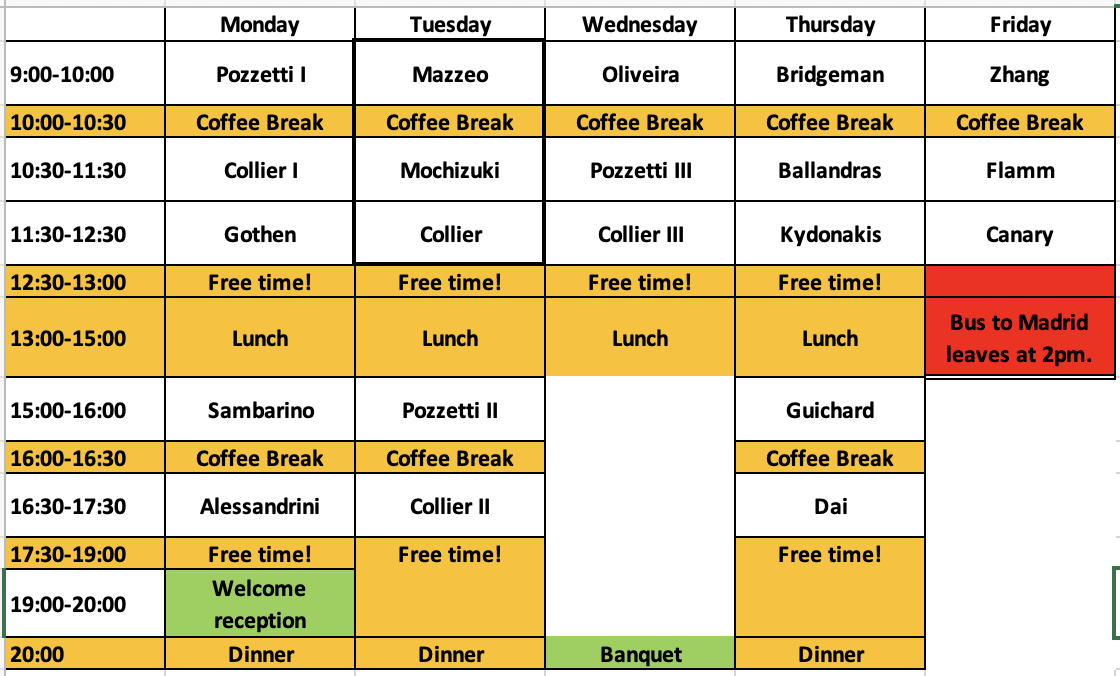
Programme
Download programme here
Titles and abstracts
Minicourses
Beatrice Pozetti (Ruprecht-Karls-Universitat Heidelberg) Positive representations
We will provide a gentle introduction to Higher Teichmuller theories: connected component of character varieties of the fundamental group of a surface of genus at least 2 in a semi simple Lie group which consist entirely of conjugacy classes of injective homomorphism with discrete image.
- Lecture 1: Hyperbolic surfaces and maximal representations
- Lecture 2: Hitchin and Anosov representatons
- Lecture 3: Theta-positive representations
Brian Collier (UC Riverside) Slodowy Slices for Higgs bundles
In this minicourse I will describe how a Higgs bundle version of the Slodowy slice through a nilpotent element of a Lie algebra can be used to parameterize interesting subsets of the character varieties of a closed surface. These subsets are determined by an sl2-subalgebra, and contain a special embedded copy of the Teichmuller space of the surface. In general, they are neither open nor closed in the character variety. However, for the special class of magical sl2 subalgebras, the Slodowy slice construction defines connected components of character varieties for certain real lie groups corresponding to positive anosov representations. Throughout the minicourse, we will focus many example of Slodowy slices both in magical case and other interesting cases. The first lecture will introduce all of the important players: Higgs bundles, character varieties and how they are related. In the second talk we will define the Slodowy slice and explore many examples with vector bundles. In the third talk we will focus on the class of magical sl2 triples and describe the special features which lead to connected components, we will also indicate what aspects may generalize to interesting, nonmagical, settings.
- Lecture 1: Character varieties and Higgs bundles
- Lecture 2: Slodowy slices with lots of examples
- Lecture 3: Slodowy slices for magical sl2-triples and positive representations
Research talks
Monday, 11:30
-
Peter Gothen (Universidade do Porto) Twisted equivariant bundles on coverings and the Hitchin-Kobayashi correspondence for non-connected groups
- Higgs pairs with non-connected structure group often appear in the study of moduli spaces of Higgs bundles for connected groups. For example, the Higgs bundle description of some higher Teichmuller spaces involves twisted G-Higgs bundles, for a Cayley partner group G which may be non-connected. One approach to the Hitchin-Kobayashi correspondence for general Higgs pairs with non-connected structure group on a Riemann surface is via so-called twisted equivariant bundles on coverings (where ”twisted” has a different meaning from that of the previous paragraph). I will explain this and report on work in progress on the Hitchin-Kobayashi correspondence in this setting. The talk is based on joint work with G. Barajas, O. Garcia-Prada and I. Mundet.
Monday, 15:00
-
Andres Sambarino (CNRS - Sorbonne Universite) Pressure degenerations are Lie-theoretic
- Via thermodynamics, the Hitchin component of a closed surface S with values on an adjoint simple-split real group, is naturally equipped with a (rank-1)-parameter family of MCG(S)-invariant bi-linear symmetric forms. These are called pressure forms and where introduced in collaboration with M. Bridgeman, D. Canary 3 and F. Labourie in 2013. In that paper it is also established the pressure form associated to the spectral radius’ is Riemannian. In this lecture we will explain a recent result on the classification of the degeneration locus of any of the pressure forms, how it relates to Lie theory and some geometric motivations for their study.
Monday, 16:30
-
Daniele Alessandrini (Columbia University) Domains of discontinuity for Anosov representations
- The parameter spaces of Anosov representations can usually be seen as deformation spaces of parabolic geometric structures on some closed manifolds, this is due to Guichard-Wienhard and Kapovich-Leeb-Porti. A particularly interesting case is given by the Higher Teichm ̈uller Spaces, spaces that generalize the classical Teichm ̈uller spaces for higher rank Lie groups. In this talk we will present a general structure theorem about the topology of such closed manifolds, and we will describe this topology explicitly in some interesting cases.
Tuesday, 09:00-13:00 Spanish Colloquium on Higgs Bundles and Minimal Surfaces
Tuesday, 09:00-10:00
-
Rafe Mazzeo (IStanford) [ZOOM] The extended Bogomolny equations and minimal Lagrangians
- I will report on a series of papers, initiated by S. He and myself and continued in the thesis of Dimakis, where large families of solutions of a certain monopole equation on the product of a Riemann surface and a half-line are produced; these families are shown to parametrize some interesting minimal Lagrangian submanifolds in the Hitchin moduli space.
Tuesday, 10:30-11:30
-
Takuro Mochizuki (Kyoto University) [ZOOM] Harmonic bundles, non-degenerate symmetric pairings, and some applications
- We shall discuss (1) the existence of a harmonic metric for a generic Higgs bundle with a non-degenerate symmetric pairing, (2) the convergence of large-scale solutions of the Hitchin equation, and (3) the estimate of the difference of the Hitchin metric and the semi-flat metric on a Zariski open subset of the moduli space of Higgs bundles. We would like to explain the key roles played by globally or locally defined non -degenerate symmetric pairings in the study of these issues. This talk is partially based on joint works with Qiongling Li and Szilard Szabo.
Tuesday, 11:30-12:30
-
Brian Collier (UC Riverside) Higgs bundles and cyclic surfaces
- Higgs bundles played a crucial role in the formulation of Labourie’s conjecture and in its proof for rank 2 groups. The key feature in rank 2 is that the minimal surface always lifts to a particular homogeneous space which fibers over the symmetric space (the cyclic space). In this talk I will discuss a class of minimal surfaces in the symmetric space of the split real form of G2 which lift J-holomorphic curves in the pseudo-Riemannian 6-sphere. These surfaces determine (and are determined by) Higgs bundles with a cyclic group symmetry. For G2 Hitchin representations these are exactly the cyclic surfaces considered by Labourie, but in general little is known about the representations which give rise to such surfaces.
Wednesday, 09:00
-
Andre Oliveira (Universidade do Porto) Components of Higgs bundles moduli spaces: old and new
- I will give an overview on the method, pioneered by Hitchin and used extensively in the last two decades, for detecting connected components of the moduli spaces M(G) of G-Higgs bundles, over a compact Riemann surface, for real Lie groups G. Among those components are the higher Teichmuller components and I will also mention those in relation to magical triples. Time permitting, I will say some words on how we are trying to proceed towards showing that there are no connected components of M(G) other than the ones already known. The part of the talk related to magical triples is joint work with S. Bradlow, B. Collier, O. Garcia-Prada and P. Gothen.
Thursday, 09:00
-
Martin Bridgeman (Boston College) Ghost polygons, Poisson bracket and convexity
- Given a cyclically ordered family of geodesics G = (g1, .., gn) in the hyperbolic plane we can assign to it a correlation function TG on the space of Anosov representations of a closed surface group. The function is given by TG(ρ) = T race(p1p2...pn) where pi is the projector of ρ(gi)). We extend correlation functions to n-cyclic geodesic currents μ to give functions Tμ. We introduce a Lie algebra on the space of cyclically ordered geodesics called the ghost bracket and extend it to the space of cyclically ordered geodesic currents. Using this ghost bracket we calculate the Hamiltonians of Tμ with respect to the Atiyah-Bott-Goldman symplectic form and prove that the map μ → Tμ is a Lie algebra homomorphism from the ghost algebra to the Atiyah-Bott-Goldman Poisson structure. We generalize the convexity theorem of Kerckhoff and show that length functions of geodesic currents are convex along Hamiltonian flows for Length functions of measured laminations. We further extend a number of results of Wolpert for the Weil-Petersson form to the Anosov representation setting. This is joint with Francois Labourie.
Thursday, 10:30
-
Mathieu Ballandras (ICMAT, Madrid) Intersection cohomology of components of the moduli space of SO(n, n + 1) Higgs bundles
- We study the intersection cohomology of certain components of the moduli space of SO(n, n + 1) Higgs bundles. Under the non-Abelian Hodge correspondence they correspond to components of a character variety. These components were described by Collier, they are singular. Intersection cohomology is a cohomology theory well suited to study singular varieties. The computation of the intersection cohomology of these components relies on general technics from Kirwan which apply to any Geometric Invariant Theory quotient.
Thursday, 11:30
-
Georgios Kydonakis (Ruprecht-Karls-Universitat Heidelberg) Parahoric torsors with logarithmic Higgs fields
- A bijective correspondence between Higgs bundles and local systems over a noncompact Riemann surface has been clarified by C. Simpson through the introduction of appropriate weighted filtrations for the objects involved. We shall describe a full correspondence between a Dolbeault and a de Rham moduli space considered for general complex reductive structure groups. The language to be used will be that of parahoric group schemes in the sense of Bruhat-Tits. Based on joint woks with Pengfei Huang, Hao Sun and Lutian Zhao.
Thursday, 15:00
-
Olivier Guichard (Universite de Strasbourg) Closedness properties for positive representations
- We will explain that a little transversality of the limit of positive representations insures that this limit representation is itself positive (joint with Labourie and Wienhard). We will then explain why this transversality always holds true (joint with Beyrer, Labourie).
Thursday, 16:30
-
Xian Dai (Ruhr-Universitat Bochum) Thurston’s asymmetric metric for Anosov Representations
- In this talk, we will introduce Finsler metrics, called Thurston’s asymmetric metrics in higher Teichmuler spaces. This is a generalization of classical Thurston’s Finsler metrics on the Teichmuller space and is constructed using Thermodynamic formalism. This work is based on contruction of the pressure metrics which are Riemannian metrics in higer Teichmuller spaces studied by Bridgeman, Canary, Labourie and Sambarino. We will compare these two metrics. This is joint work with Leon Carvajales, Beatrice Pozzetti and Anna Wienhard.
Friday, 09:00
-
Tengren Zhang (National University of Singapore) Pleated surfaces in PSL(d, C)
- In this talk, we define a notion of d-pleated surfaces that generalizes the classical notion of an (abstract) pleated surface in a hyperbolic space. We then prove a that the space of d-pleated surfaces is holomorphically parameterized by cocyclic pairs, thus generalizing a theorem of Bonahon for classical pleated surfaces. This is joint work with Sara Maloni, Giuseppe Martone, and Filippo Mazzoli.
Friday, 10:30
-
Xenia Flamm (ETH Zurich) Hitchin representations over real closed fields
- The space of representations of the fundamental group of a closed surface into PSL(n,R) contains a distinguished connected component consisting entirely of discrete and faithful representations: the Hitchin component. For n=2 this component agrees with Teichmuller space and the study of its compactifications has lead to many influential results. The goal of this talk is to introduce the real spectrum compactification of the Hitchin component as defined by Burger-Iozzi-Parreau-Pozzetti, echoing the work of Brumfiel for Teichmuller space. We will explain the relevant concepts from real algebraic geometry and hint at how boundary points can be viewed as representations into PSL(n,F), where F is a real closed field extension of R, which admit positive limit maps into flag varieties over F.
Friday, 11:30
-
Dick Canary (University of Michigan) The augmented Hitchin component: a conjectural geometric picture
- The augmented Teichmuller space is obtained by adding marked nodded hyperbolic surfaces. One may think of it as the “universal cover” of the Deligne-Mumford compactification of Moduli space. Masur showed that it also arises as the metric completion of Teichmuller space with the Weil-Petersson metric. One may similarly obtain an augmented Hitchin component by appending noded Hitchin representations to the Hitchin component. It is conjectured that this augmented Hitchin component arises as the metric completion of the Hitchin component with a pressure metric. We describe this conjecture and progress in the direction of the conjecture. (This is joint work with Bray, Kao and Martone and with Zhang and Zimmer).




